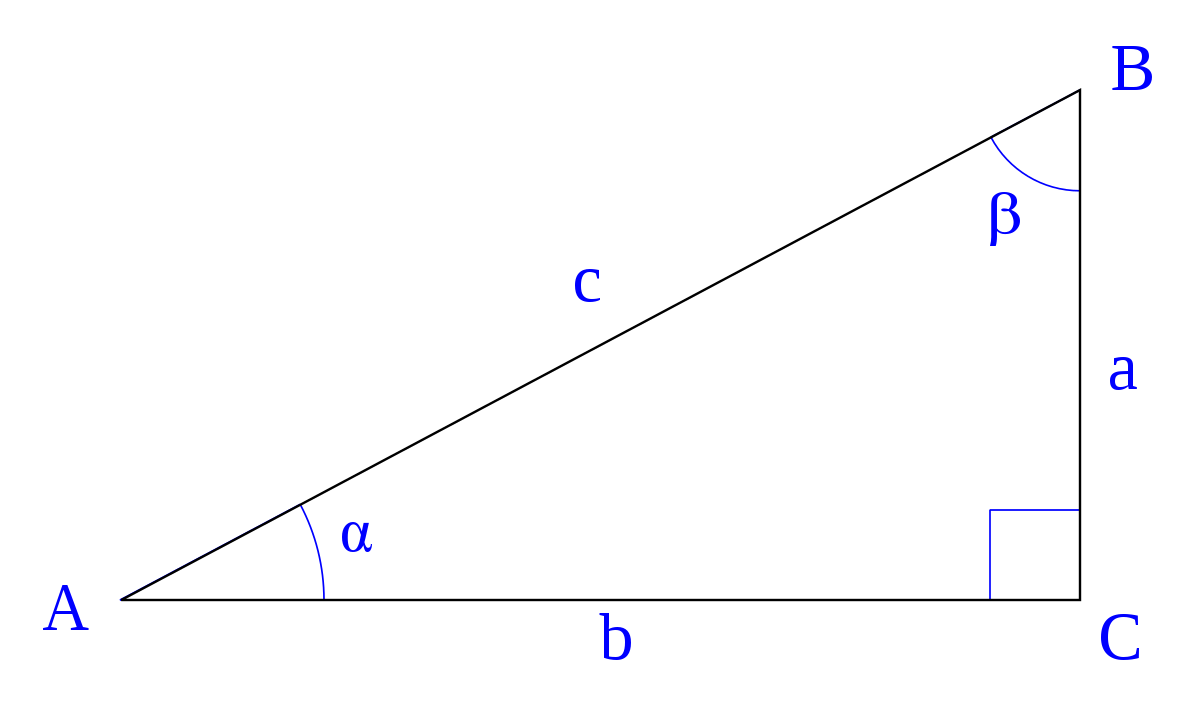
Como las razones trigonométricas solo dependen de la medida del ángulo, entonces si conocemos el valor de solo una de ellas, las restantes se pueden calcular construyendo un triángulo rectángulo Aplicaciones1 Si tana = 0,5 (a agudo), calcular csca y seca ResoluciónDato tana = 1/2 Teorema de Pitágorasc2 = 12 22 => c = V5csca ;t =Las medidas de los lados son x , , y 2 x En un triángulo 30°60°90°, la longitud de la hipotenusa es dos veces la longitud del cateto más corto, y la longitud del cateto más largo es veces la longitud del cateto más corto Para ver porque es esto, dese cuenta que Triângulos retângulos são chamados de triângulos pitagóricos quando as medidas de seus lados forem números inteiros Por exemplo, podemos tomar os triângulos com as seguintes medidas 3, 4 e 5, pois 32 42 = 52 6, 8 e 10, pois 62 = 102 5, 12 e 13, pois 52 122 = 132

Resolucion De Triangulos Rectangulos Superprof
Triangulo rectangulo notable de 15 y 75 grados
Triangulo rectangulo notable de 15 y 75 grados-Um triângulo retângulo qualquer é chamado de triângulo pitagórico caso a medida de seus lados satisfaça o teorema de Pitágoras Exemplos O triângulo acima é pitagórico, pois 5 2 = 3 2Table à manger extensible Décor chêne artisan L 1600 x P 75 x H 90 cm BERGEN 179 €99 149 €99 HT 299,00€ 249,17€ HT119€ SOLDES99€ HT SOLDES Soldes Ensemble repas de jardin 6 personnes effet ciment table 180 cm 1 lot de 6 fauteuils VULKAN (3) 349 €99 291 €66 HT 364,99€ 304,16€ HT15€ SOLDES12€ HT SOLDES Soldes DENVER Meuble TV 2 portes




Triangulos Rectangulos Notables Completo
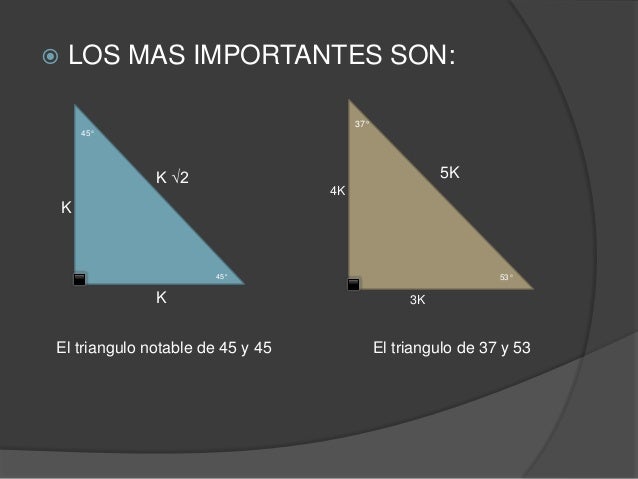
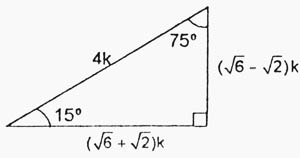
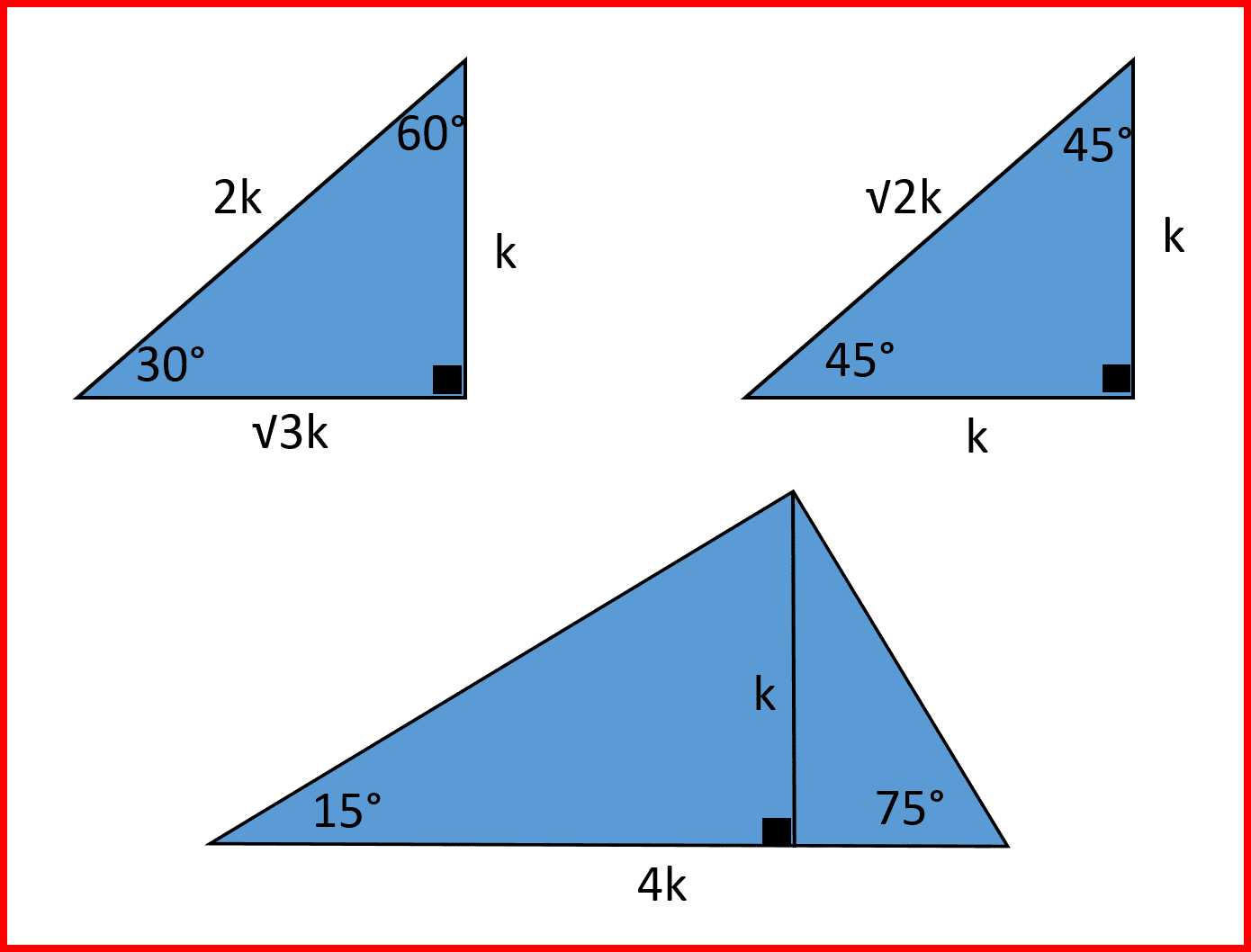
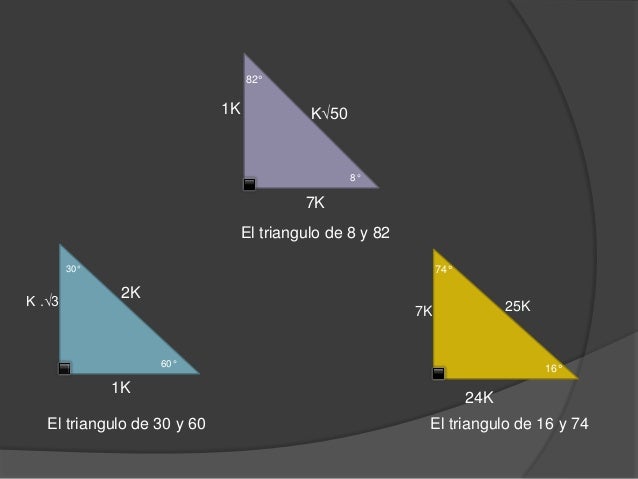
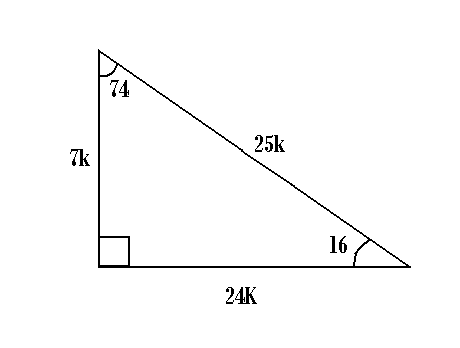
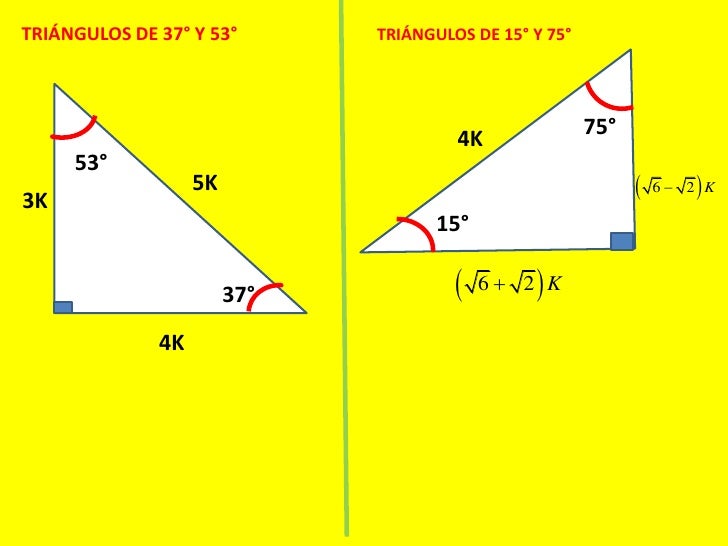
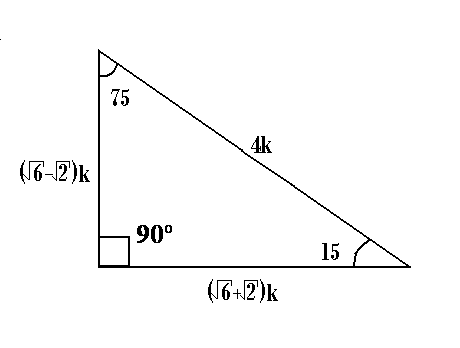
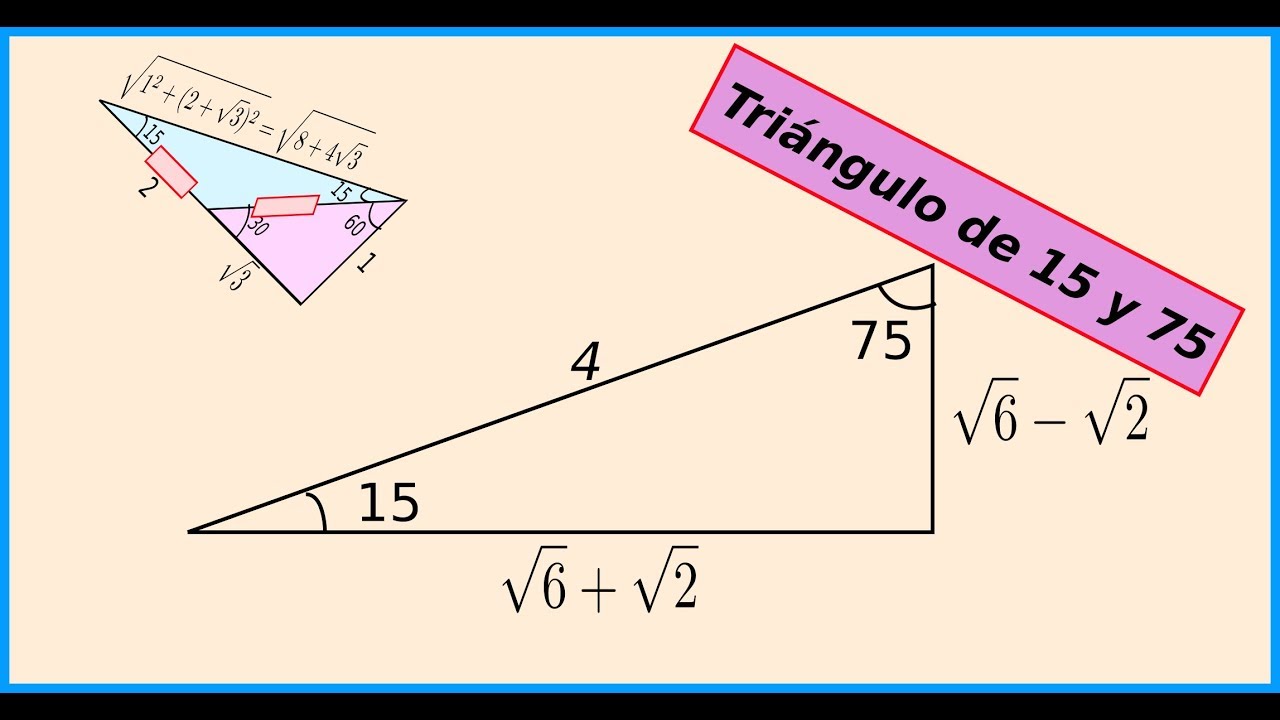
° 1K K√50 8° 7K El triangulo de 8 y 30° K √3 74° 2K 25K 7K 60° 1K El triangulo de 30 y 60 16° 24K El triangulo de 16 y 74 8 √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2 9Recherche d'adresses, de lieux, comparateur d'itinéraires pour préparer vos déplacements partout en France Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2
Haz clic aquí 👆 para obtener una respuesta a tu pregunta ️ si la base de un triangulo rectangulo mide 10cm y la altura 15 cm;Triangulo de 9,12 y 15ESTUDIO DEL TRIANGULO PITAGORICO lunes, 13 de mayo de 13 DEFINICION EL TEOREMA DE PITÁGORAS Un triángulo rectángulo es un triángulo que contiene un ángulo recto (un ángulo de 90°) El Teorema de Pitágoras es una teoría acerca de los ángulos rectos que fue descubierta alrededor de 2500 años atrás por un matemático griego llamado Pitágoras Esta teoría se llama
El triángulo de 15 y 75 grados Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up Next Tras regresar a Samos, finalizó sus estudios, según Diógenes Laercio con Hermodamas de Samos y luego fundó su primera escuela durante la tiranía de Polícrates Abandonó Samos para escapar de la tiranía de Polícrates y se estableció en la Magna Grecia, en Crotona alrededor del 525 a C, en el sur de Italia, donde fundó su segunda escuela Las doctrinas deProfe, la ecuación del plano es x/177 y/240 z/44 = 1 Nina me enseñó su "colección" de triángulos pitagóricos Tal "colección" era en realidad puntos en el plano El triángulo rectángulo de catetos 3 y 4 (la cuerda de doce nudos) estaba representado por el punto de




Todo Los Triangulos Notables Sus Angulos Medidas




Calameo Geometria 8
De todo modo, esse texto estudar exatamente a rica situao de triplas de nmeros inteiros, chamadas de Triplas Pitagricas, ou seja, triplas de nmeros inteiros que podem representar as medidas dos lados de um tringulo retngulo Por exemplo, mais dois exemplos 6, 8, 10 e 9, 12, 15 Embora triplas pitagricas so meio que um plgio da tripla 3, 4 e 5, pois representam tringulos retngulos com aPágina de estudos de matemática e sequências numéricas Ternos pitagóricos e os ângulos de triângulos retângulos 070 Os ternos pitagóricos quando aplicados em modelos matemáticos utilizando as figuras geométricas de triângulos retângulos observase regularidades quanto aos ângulos desses mesmos triângulos retângulos(4) Postgraduado A = 15°, (90° A) = 75° Las deducciones y tabla anteriores un procedimiento estándar en cualquier curso o texto de trigonometría Sin embargo observará los huecos entre 0° y 30°, y entre 60° y 90° Si queremos que el ángulo A se incremente en pasos iguales de 15 o, necesitaremos los senos y cosenos de 15° y 75°




Triangulo Notable De 15º Y 75º Demostracion Youtube




Triangulos Rectangulos Notables Matemath Web
Teorema de Pitágoras en un Triángulo 45º,90º,45º En cualquier cuadrado al trazar una diagonal se obtienen dos triángulos Estos triángulos son rectángulos y sus ángulos miden 45º,90º, y 45º Arrastra los puntos A, o B, para modificar las dimensiones del triángulo observa lo que sucede con la división hipotenusa/catetoSu area es de 75 cm elevado al cTenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el ángulo de 75°, puede ser generado por la suma de 30° más 45° Ahora, habría que preguntarse si existe otro ángulo (comprendido dentro del primer cuadrante) que genere un valor exacto para las funciones seno y coseno aparte de los ya conocidos hasta ahora Ese ángulo existe y es lo que vamos a




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Rectangulo Worksheet
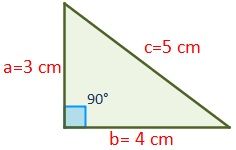
El área de un triángulo es base ( b b) por altura ( a a) divido entre 2 Como sabemos que el área es 15 c m 2 15 c m 2 y que la base es b = 6 c m b = 6 c m, podemos calcular la altura La altura del triángulo es 5cm Finalmente, calculamos la hipotenusa aplicando Pitágoras La hipotenusa mide, aproximadamente, 781cmAchat et vente en ligne parmi des millions de produits en stock Livraison gratuite à partir de 25€ Vos articles à petits prix culture, hightech, mode, jouets, sport, maison et bien plus !Usa el teorema de Pitágoras para determinar si un triángulo con lados de 15 cm, 7 cm y 16 cm es un triángulo rectángulo 2 Ver respuestas kjhnladen kjhnladen Respuesta Hola!



Triangulos Notables




Teorema De La Suma De Un Triangulo Ck 12 Foundation
El Teorema de Pitágoras Página 30 Ejercicio 75 Calcula la distancia, en milímetros, entre los puntos A y B en un prisma recto de base cuadrada, siendo el lado de la base de 8 cm y la altura del prisma de 12cm Solución AB=132,7mm Ejercicio 76 En un prisma recto, de altura 15 cm, la base es un triángulo equilátero de lado 10 cm En él se han marcado un vértice A y el centro B de laExplicación paso a paso Si (7 cm) ² (15 cm) ²= (16 cm)², entonces este es un triángulo rectángulo, según el teorema de Pitágoras De lo contrario no lo es 15 ² 7 ²= 225 49 = 1225 = 35 ² Esto esTriángulo Pitagórico Autor JL En este enlace se muestra la construcción final de los dos triángulos Como se puede observar son triángulos rectángulos semejantes (misma forma) Prueba a arrastrar el punto B y verás cómo los triángulos se mantienen en la misma proporción Como podrás observar si modificas la posición del punto B a lo largo del eje




Resuelve El Siguiente Tr Descubre Como Resolverlo En Qanda




Las Ternas Pitagoricas Y Fibonacci Matematicascercanas
Es decir, que pueden formar tripletes pitagóricos, de modo que a 2 = b 2 c 2 Así, en una cuerda cerrada de 12 nudos separados entre sí una misma distancia, los nudosNúmeros Pitagóricos o Ternas Pitagóricas Son una tripleta de números naturales (enteros positivos) a, b, c, que cumplen que la suma de los cuadrados de los dos menores, equivalen al cuadrado del número mayorSi los dos menores de la tripleta son a y b, entonces a 2 b 2 = c 2 Geométricamente una terna pitagórica se corresponde con un triángulo rectángulo donde la medida deAvec leboncoin, trouvez la bonne affaire, réalisezla bonne vente pour votre voiture, immobilier, emploi, location de vacances, vêtements, mode, maison, meubles, jeux vidéo, etc, sur le site référent de petites annonces de particulier à particulier et professionnels




Triangulos Rectangulos Notables Matemath Web




Triangulos Notables Estudiandoenlinea
O segundo trio pitagórico que aparece comumente é (5 2 12 2 = 13 2, 25 144 = 169) Esteja também atento para múltiplos, como , e divisores, como 2,566,5 2 Memorize as proporções de um triângulo retângulo Um triângulo retângulo Um triângulo retângulo pitagórico possui 15 unidades como hipotenusa, determine os seus catetos IsabelValdim está aguardando sua ajuda Inclua sua resposta e ganhe pontos Novas perguntas de Matemática Um triângulo retângulo pitagórico possui 15 unidades como hipotenusa, determine os seus catetos 100 60 (9 5 2) x 3 me ajuda pfvvvvvvvvvvvvvvv Em uma provaY, de hecho, es válido para todos los triángulos rectángulos El Teorema de Pitágoras puede también representarse en términos de área En un triángulo rectángulo, el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos Puedes ver la ilustración siguiente para el mismo triángulo rectángulo 345 Observa que el Teorema de Pitágoras




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Rectangulos Notables Matemath Web
Triángulo pitagórico Triángulo pitagórico, también denominado triángulo de Plutarco o triángulo diofántico, es todo aquel en el que sus lados (a, b, c) son números enteros;Por TadeoNieto07 Inicia sesión para añadir comentario Respuestas tiamosi Genio;Triángulo pitagórico Demostración con Áreas del teorema de Pitágoras Los áreas de los cuadrados representan el valor de los lados al cuadrado a los que hace referencia el teorema El punto de la derecha puede desplazarse en el eje x A parte de la configuración inicial del triangulo con lados 3, 4 y 5



Triangulo Rectangulo Rotacion Y Escala Geogebra



Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze
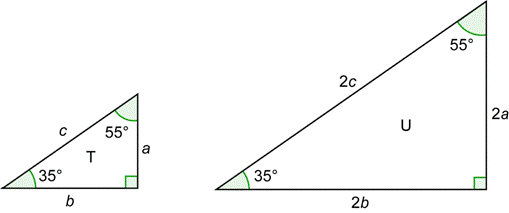
Un triángulo rectángulo tiene una hipotenusa de 15 m y una base de 9 m Determina el área del triangulo Pide más detalles ;Solución r = b' b r = 3 2 = 1,5 a' = 1,5 2,5 = 3,75 cm c' = 1,5 3 = 4,5 cm 4 El 3erángulo del 2º triángulo mide 180° – (75° 60°) = 180° – 135° = 45° Es decir,los ángulos del 2º triángulo miden 45°,60° y 75° Como los dos triángulos tienen sus ángulos iguales, son semejantes b' = 3 cm cO mesmo é verdade para e até mesmo para 1,522,5 Faça os cálculos e veja por conta própria!



Triangulo Rectangulo Problema 7 Basico



Unidad Vii Geometria Trigonometria Y Series
Trios pitagóricos ¶ Un trío pitagórico se define como un conjunto de tres números, a, b y c que cumplen con la relación a2 b2 = c2 Desarrolle un programa que contenga la función son_pitagoricos (a, b, c) que retorne True si a, b y c son un trío pitagórico, y False si no lo son >>> son_pitagoricos(3, 4, 5) True >>> son_pitagoricos(4, 6, 9) Lo bueno, malo y feo de la capacitación a directores Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2Por el teorema de Pitágoras c² = a²b² 15² = a²9² 225 = a²81 = a² 144 = a² a = √144 a = 12 La formula del area de un triangulo
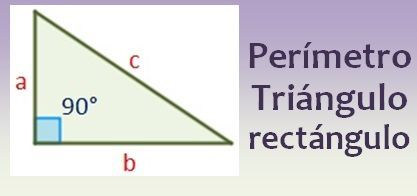



Perimetro De Un Triangulo Rectangulo




Perimetro De Un Triangulo Rectangulo
Teorema de la altura y de los catetos de un triángulo rectángulo Sea el triángulo rectángulo ∆ ABC , ºAˆ =90 Sea la altura h =AH sobre la hipotenusa Sea m =BH la proyección del catetos c sobre la hipotenusa Sea n =HC la proyección del catetos b sobre la hipotenusa Entonces, a) nh2 =m⋅ Teorema de la altura b) b2 =n⋅a Teorema del cateto c) ac2 =m⋅ Teorema del catetoUn triángulo racional se puede definir como uno que tiene todos los lados con longitud racional, si bien cualquier triángulo racional de este tipo se puede volver a escalar (puede tener todos los lados multiplicados por el mismo entero, es decir, un múltiplo común de sus denominadores) para obtener un triángulo entero, por lo que no hay diferencia sustancial entre triángulos enteros y En el antiguo Egipto, el triángulo de proporciones 345 más utilizado en arquitectura y agrimensura era el de lados iguales a 15, y 25 codos respectivamente (unos 75,
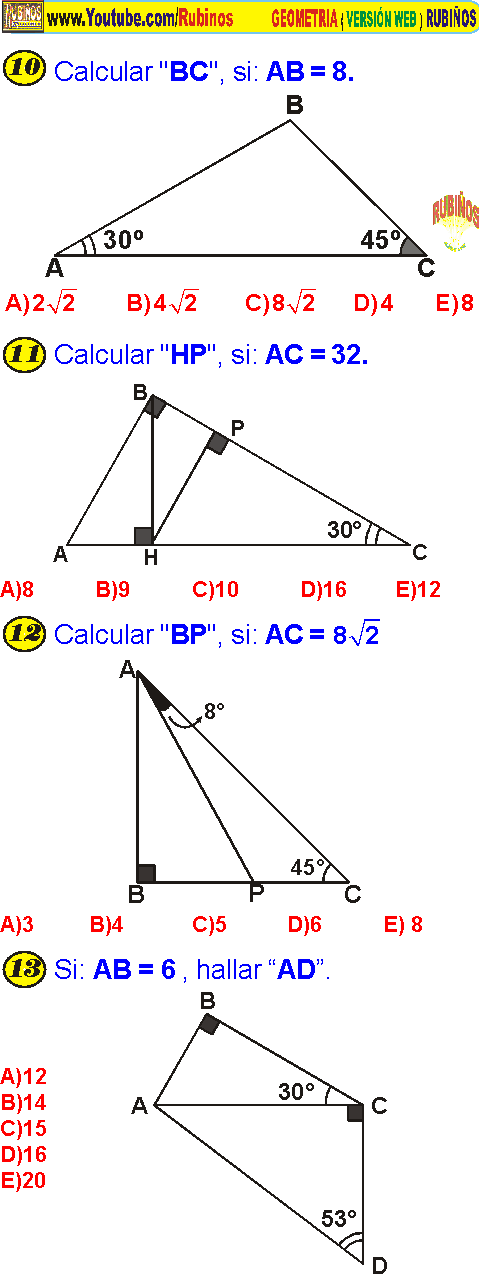



Triangulos Notables Ejercicios Resueltos Pdf




En Un Triangulo Rectangulo La Cotangente De Uno De Sus Angulos Agudos Es 0 75 Calcular La Brainly Lat




La Formula De Heron Para El Area De Un Triangulo Y Resolver Problemas Con Trigonometria Ck 12 Foundation




Usar La Ley De Cosenos Con Lal Para Encontrar El Tercer Lado Ck 12 Foundation




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos




Triangulos Rectangulos Notables Matemath Web




Triangulos Rectangulos Notables Completo




Perimetro De Un Triangulo Rectangulo
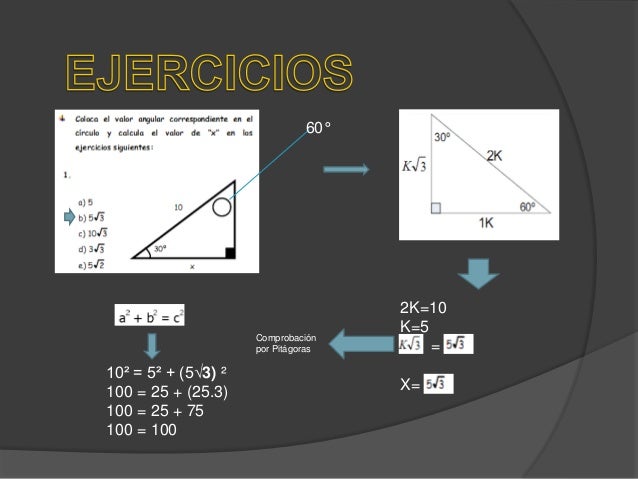



Triangulos Notables




Perimetro De Un Triangulo Rectangulo




Resolucion De Triangulos Rectangulos Superprof




41 Ideas De Computacion Razones Trigonometricas Computacion Calcular El Area
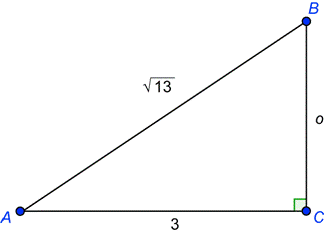



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y




41 Ideas De Computacion Razones Trigonometricas Computacion Calcular El Area




Triangulos Notables Ejercicios Resueltos Pdf




Triangulos Notables Estudiandoenlinea




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Resueltos Pdf




Resolucion De Triangulos Rectangulos Superprof




Como Encontrar La Longitud Del Lado De Un Triangulo Rectangulo



Resolucion De Triangulos



18 Problemas Sobre Triangulos Rectangulos



Perimetro De Un Triangulo Rectangulo




Triangulos Notables Estudiandoenlinea




Triangulo Notable De 15 Y 75 6 Youtube



Triangulos Notables




Ejercicios Con Triangulos Oblicuangulos Superprof



Terna Pitagorica Wikipedia La Enciclopedia Libre




Los Catetos De Un Triangulo Rectangulo Miden 3 Cm Y 4 Cm Respectivamente Cuanto Mide El Coseno Del Menor Angulo 3 Sin A 5 4 Cos A Pdf Descargar Libre




Ejercicios Resueltos Del Teorema De Pitagoras Lecciones De Mates



File Triangulo Auxiliar De 74 Y 16 Png Wikimedia Commons



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf



Triangulo Rectangulo



Www Uv Es Lonjedo Esoproblemas 3eso14triangulo Pdf




Triangulos Notables Estudiandoenlinea
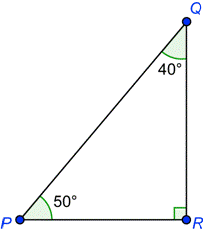



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y
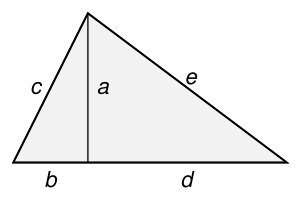



Triangulo Entero Wikipedia La Enciclopedia Libre




Halla Las Medidas De Los Angulos De Un Triangulo Rectangulo Sabiendo Que La Hipotenusa Y Uno De Los Brainly Lat




Ley De Los Senos



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Triangulos Rectangulos Notables Matemath Web




La Medida De Uno De Los Angulos Agudos De Un Triangulo Rectangulo Es El Quintuplo Del Otro Halla La Brainly Lat



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y
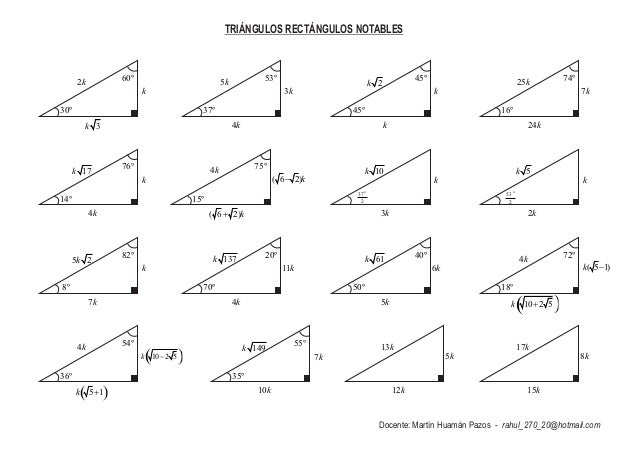



Triangulos Rectangulos Notables Completo




Teorema De La Suma De Un Triangulo Ck 12 Foundation




Resolucion De Triangulos Superprof



Deducciones Del Teorema De Pitagoras A Lo Largo De La Historia Como Recurso Didactico En El Proceso De Ensenanza Aprendizaje De La Matematica
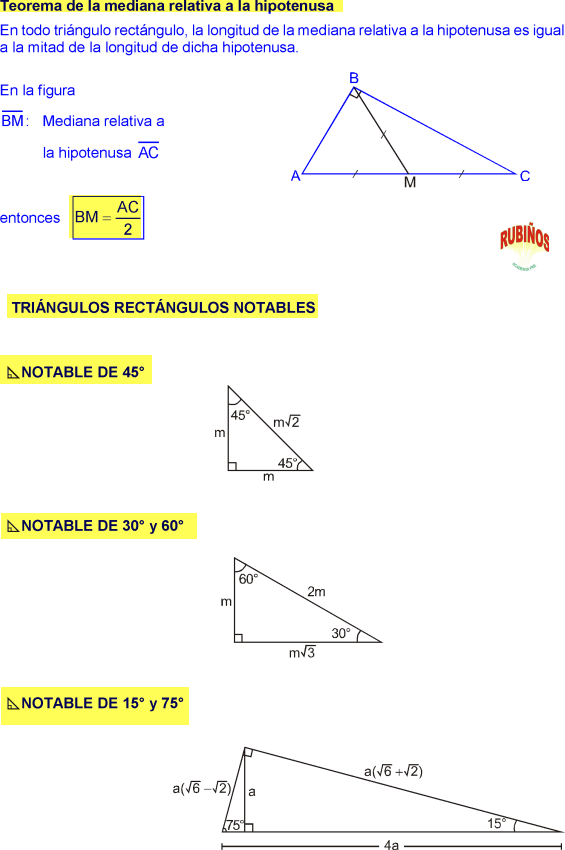



Congruencia Triangulos Ejercicios Resueltos




Se Sabe Que La Suma De Los Angulos Internos De Un Triangulo Mide 1800 En Un Triangulo Rectangulo Uno Brainly Lat




Triangulo Rectangulo




Todo Los Triangulos Notables Sus Angulos Medidas




Ley De Los Senos




Dos Angulos Complementarios De Un Triangulo Rectangulo Estan Relacionados Asi Uno De Ellos Es Cinco Brainly Lat




Triangulos Notables Ejercicios Resueltos Pdf




Clasificacion De Triangulos Segun Los Angulos Ck 12 Foundation
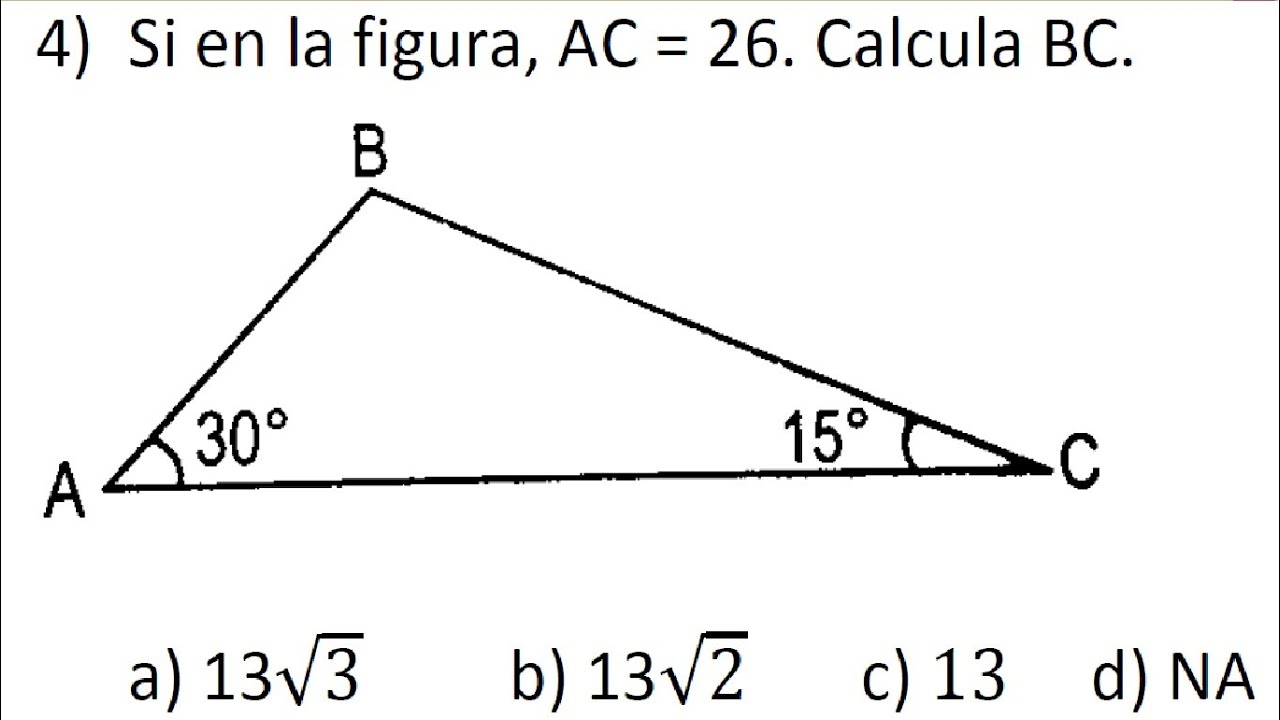



Triangulo Rectangulo Notable 15 Y 75 Youtube



Triangulo Rectangulo Docsity




Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy




Problema 434
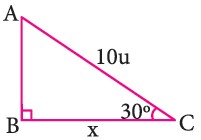



Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y



Triangulos Notables Ejercicios Resueltos Pdf




Resolucion De Triangulos Superprof



Archivo Triangulo Auxiliar De 75 Y 15 Png Wikipedia La Enciclopedia Libre



Www Unirioja Es Talleres Creatividad Matematica Seminariobachillerato Recursosgeometria Pdf




Relaciones Metricas En El Triangulo Rectangulo Geometria 5to Secundaria Triangulo Geometria Del Plano Euclidiano




Triangulos Rectangulos Notables Matemath Web



Triangulos Notables Ejercicios Resueltos Pdf



Www Matematicasonline Es Segundoeso Ejercicios Pitagoras Cuadernillo Pdf
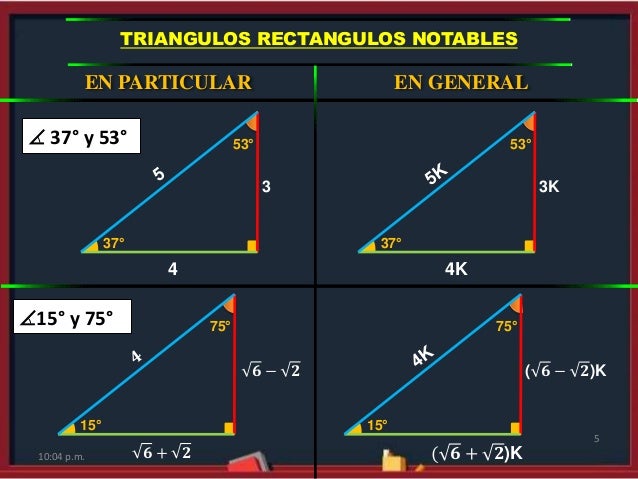



Triangulos Rectangulos Notables




Triangulos Rectangulos Notables Matemath Web



Http Fcaglp Unlp Edu Ar Area Docente Ingreso 14 Modulos 14 Modulo 5 Trigonometria Pdf




Teorema De La Suma De Un Triangulo Ck 12 Foundation




Construyendo Triangulos Pitagoricos Truco Matematico Youtube
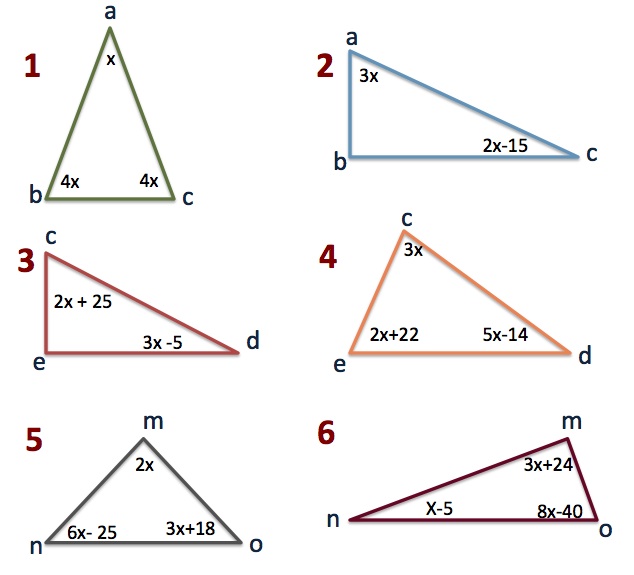



Algebra Triangulos Y Ecuaciones Spanish Ged 365




Todo Los Triangulos Notables Sus Angulos Medidas



Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado




Triangulo Rectangulo Notable De 15 Y 75 Youtube
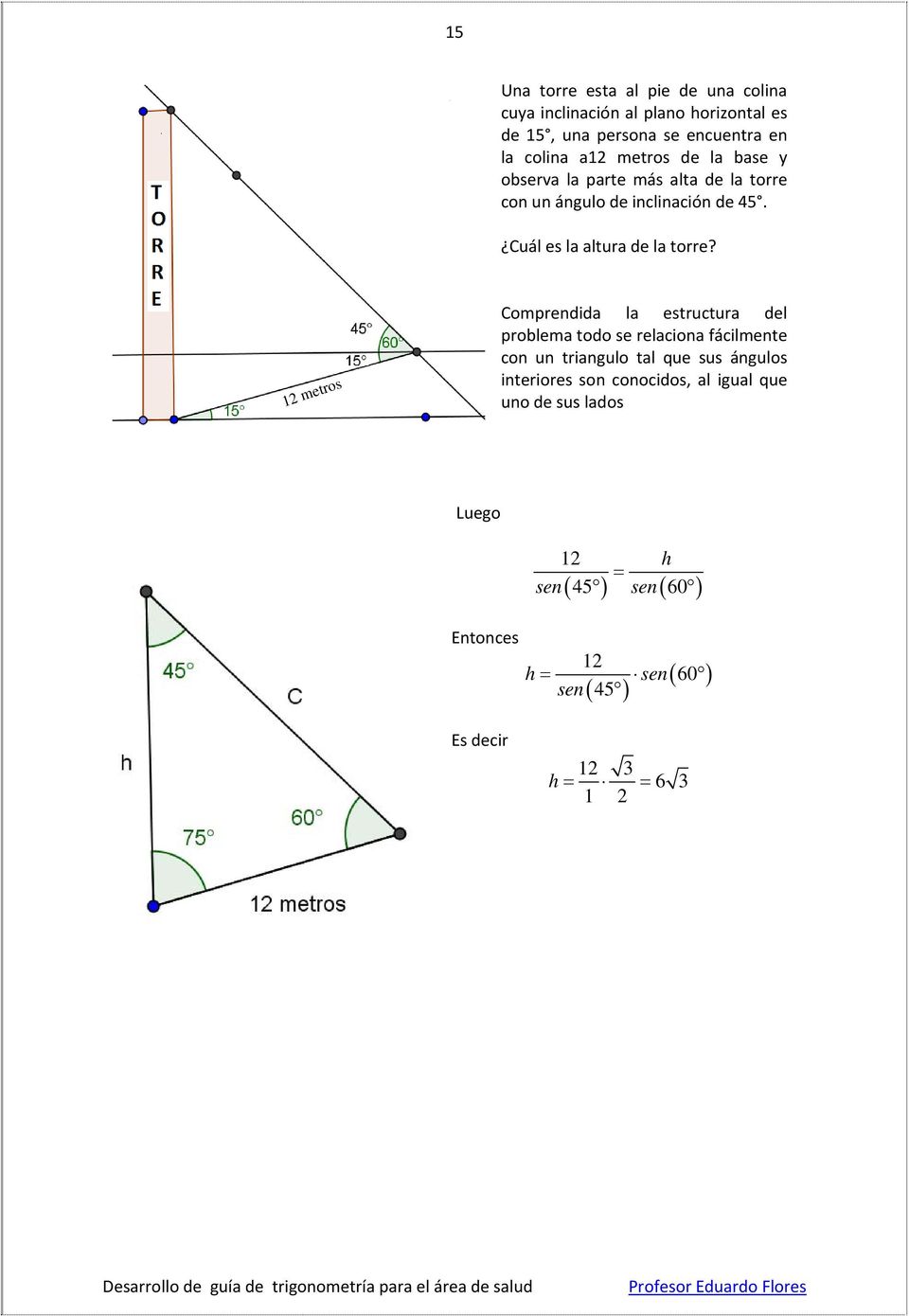



Los Catetos De Un Triangulo Rectangulo Miden 3 Cm Y 4 Cm Respectivamente Cuanto Mide El Coseno Del Menor Angulo 3 Sin A 5 4 Cos A Pdf Descargar Libre



El Triangulo De 15 Y 75 Grados Youtube



0 件のコメント:
コメントを投稿