いろいろな三角関数 関数 y = sin ( θ − π 3 ) {\displaystyle y=\sin \left(\theta {\frac {\pi }{3}}\right)} のグラフは、 y = sin θ {\displaystyle y=\sin \theta } のグラフを θ軸方向に π 3 {\displaystyle {\frac {\pi }{3}}} だけ平行移動させたものになり、周期は 2 π {\displaystyle 2\pi } である。岐阜数学教育研究 11, Vol 10, 3649 「いろいろな事象と関数」における教材の提案 中牧卓也1,愛木豊彦1,畑中裕史2, 平成24 年4 月から全面実施される学習指導要領中学校数学科の関数領域に,中学3 年で 学習する内容として「いろいろな事象と関数」が新規に追加された。数学 いろいろな関数の導関数 Archive HOME 高校数学 高校数学の基本問題 presented by 高校無料問題プリント 高校1年から3年までの数学主要単元を網羅している無料問題掲載サイトです。具体的な解説からはじまり、簡単ないくつかの例題の出題後、本当の問題が掲載されています。 続きは

麻生雅久の数学なるほど数学iiいろいろな関数 図形と式a Soの解法 試験で点がとれる 大学受験v Books 麻生 雅久 本 通販 Amazon
いろいろ な 関数
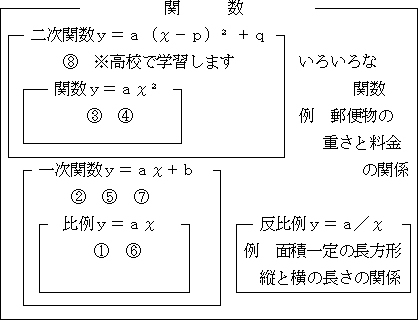
いろいろ な 関数-いろいろな関数 数量の関係を1つの式で表せなく、定義域を分けて、各定義域ごとの関数を考える問題です。 ガウス関数という高校数学で詳しく学びますが、中学では郵便物や駐車場の料金などのグラフの問題が出題されます。 具体的な問三角関数のグラフ(2) いろいろな三角関数のグラフ はじめに(4分38秒) y軸方向に拡大・縮小した三角関数のグラフ(3分32秒) θ軸方向に拡大
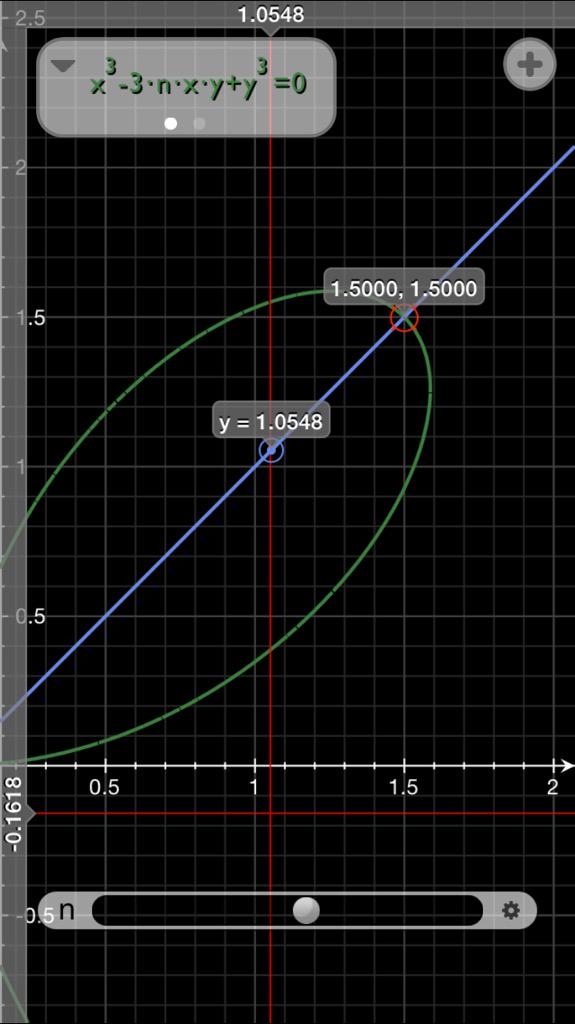



いろいろな関数
F (x) f (x) が三次以下の関数のとき, ∫ a b f ( x) d x = ( b − a) 6 { f ( a) 4 f ( a b 2) f ( b) } \displaystyle\int_a^bf (x)dx=\dfrac { (ba)} {6}\ {f (a)4f (\dfrac {ab} {2})f (b)\} ∫ ab f (x)dx = 6(b− a) {f (a)4f ( 2a b )f (b)}いろいろな 関数 ~グラフを 利用 して 解決 しよう ~ <教材観 > 高等学校 の数学 においては 、1次関数 、2次関数 を始めとして 様々な関数 を学習 する 。そこ ではグラフで 表現 することが 非常 に有効 となる 。今回 は携帯電話 の通話 料や水道料金理論いろいろな関数 コース 徹底攻略中学数学 中学数学のインプット系講義です。中学数学の全範囲を網羅し、徹底解説しています。準拠教材も講師HPにて公開しているので、併せて活用してください。 マスティー 受講者 前の動画 関連動画 理論2乗に比例する関数 理論2乗
$\sin mx$ は奇関数, $\cos nx$ は偶関数であるから $\sin mx\cos nx$ は奇関数になります。よって よって $\displaystyle \int_{\pi}^{\pi} \sin mx\cos nx~dx=0$いろいろ ろな関数 (本時) グラフが階段状になる関数について、値の変化を調べたり、同様の関数と値を な関数 比較し考察したりすること 章の問題A 第 時12 2 y = a χいろいろな原始関数の求め方 作成者 Bunryu Kamimura ジオジェブラには微分と積分の関数がついています。 Integral(関数)で原始関数を求めることができます。 いろいろ試してみましょう。 次へ 原始関数の求め方 新しい教材 2次関数のグラフ;
35 いろいろな関数のグラフ p46 第2次導関数と曲線の凹凸 漸近線 分数関数のグラフ 無理関数のグラフ 三角関数のグラフ 指数関数のグラフ 対数関数のグラフ 対称性 36 物理的思考 p55 1次元の運動 2次元の運動 さまざまな量の変化率 37 近似式 p57 1次式近似いろいろな関数の導関数 1 三角関数の導関数 三角関数の導関数 1 例題 解 問1 問2 数学III Advanced 4章「微分」 2 (教科書p151) 対数関数 log 𝑎𝑥 の 𝑥= 1 における微分係数を考えてみよう。 lim ℎ→0 log𝑎(1 ℎ) −log𝑎1 ℎ = limℎ→0 1 ℎ log𝑎(1 ℎ) = lim ℎ→0 log𝑎(1 ℎ) 1 ℎ この値をいろいろな関数の導関数 (関数の組合せ)・・・問題数が多いので,必ずしも全部を解く必要はありません。 「ある範囲までは習っているが他の範囲は習っていない」というような場合に,範囲を制限した問題練習が可能です。 計算用紙は必要です・・・現役生徒が手ぶらで解くのは無理
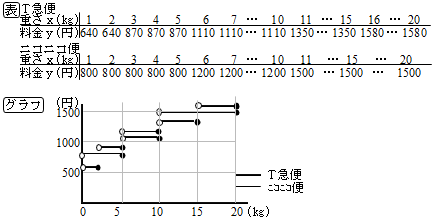



授業実践記録 数学 関数の考えを用いて主体的に問題を解決しようとする態度を育てる学習指導 啓林館
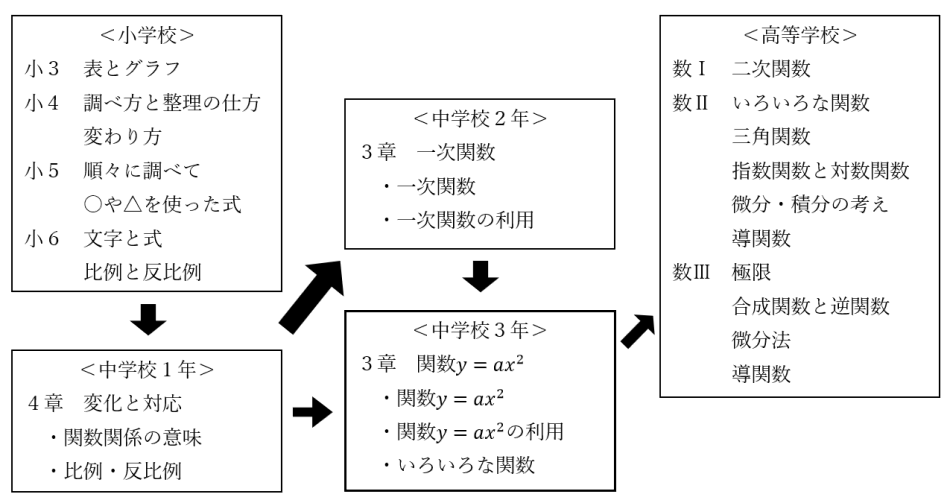



第2学年 一次関数 単元を貫く導入課題 授業実践記録 アーカイブ一覧 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館
いろいろな級数 ここでは、いろいろな級数を紹介してみたいと思います。 1つ目は、無限和が円周率を4で割った値になる級数です。 これは、1673年にライプニッツが発見した公式ですが、実際には、1400年ころ、マーダヴァ(インドの数学者)により、最初3章 関数とグラフ §2 いろいろな関数 (p87 ~p97) (1) この関数 のグラフは,y = x3 のグラフをx 軸方向に ¡2,y 軸方向に1 平行移動したものである. また,x = 0 のとき y = (02)3 1 = 81 = 9 ¡2 1 9 x y O (2) この関数のグラフは,y = ¡x3 のグラフをx 軸方向 に1,y 軸方向に¡3 平行移動したものShare your videos with friends, family, and the world




合成関数とは 数 いろいろな関数 現大手予備校講師の5分でわかる 高校数学 Youtube
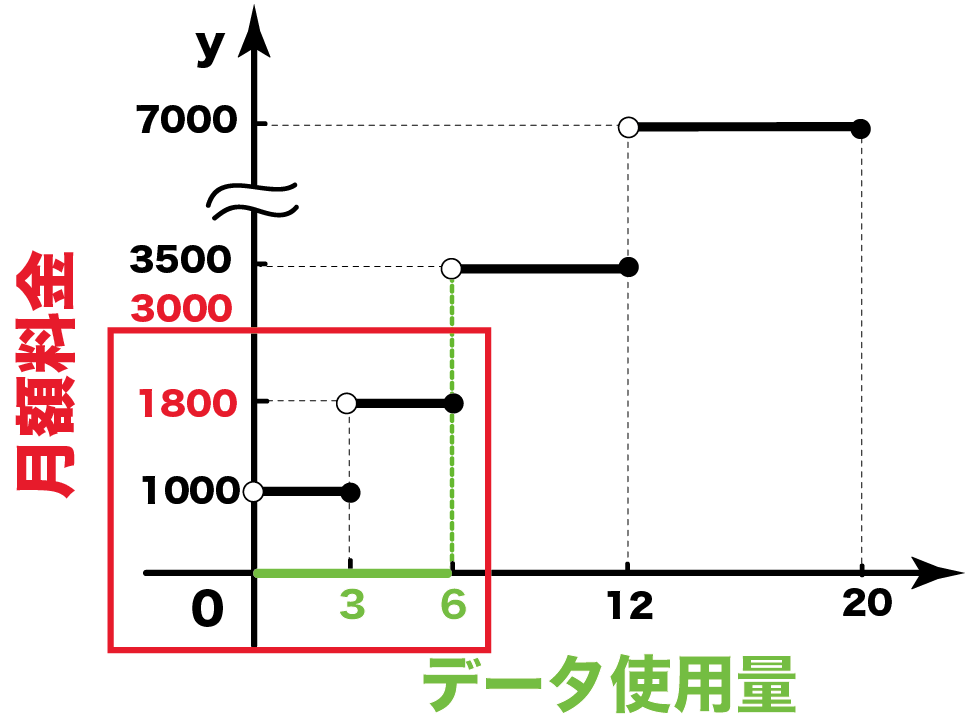



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
メビウス関数 : n が 平方因子 を持つ数ならば μ ( n) = 0、 n が相異なる 偶数 個の素数の積ならば μ ( n) = 1、 n が相異なる 奇数 個の素数の積ならば μ ( n) = −1 と n によって3通りの値をとる関数。 ゼータ関数 およびその類似物である L関数 :これらの関数と素数の間に深い関係があることは、 リーマン予想 で示唆されている。 リーマン予想 を仮定すると 素数のいろいろな曲線の確認 ★いろいろな曲線の代表的なものを確認しておこう。 余擺 よはい 線 せん とも。半径a の円がx 軸上を滑らずに転がると き、円の周上の定点P の描く曲線。エピトコロイド、ハ イポトコロイドも各サイクロイドのものにつながる。 sin第二次 関数の値の変化・・・4時間 第三次 いろいろな事象と関数・・・4時間(本時は第2時) (4)本時の目標 関数のグラフを個人や班員と求める活動を通して,次のことをできるようにする。 比例や一次関数を活用して課題を解決しようとしている。




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




いろいろな関数 無料で使える中学学習プリント
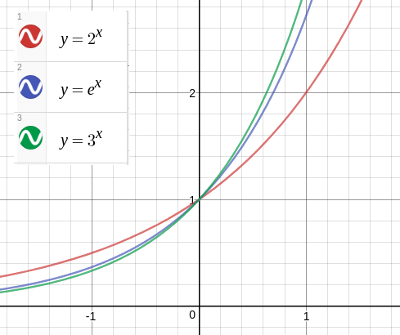
Xの関数であるyの具体例を紹介しよう。 中学1年生では、 y = 2 x のようなシンプルな関数が登場するよ。 この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、 xに「3」を入れると、yは「6」になるね。 xに何をぶち込むかによって、yの値がちがう。Try IT(トライイット)のいろいろな関数の導関数の問題の様々な問題を解説した映像授業一覧ページです。 いろいろな関数の導関数の問題を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧ください。 ピックアップ映像授業 問題 合成関数の微分(2) 高校数学Ⅲ 問題 d/dx,d/dyについて(1) 高校数学Ⅲカーネル関数は他にもいろいろな手法にも使えます。変数間の非線形性を考慮するための便利な関数です。カーネル関数、最高! たとえば SVM では、次のような文脈でカーネル関数が出てきます。 線形の SVM モデルを定式化できた (式で表せた)! ↓ 目的変数 y と説明変数 x の非線形関




いろいろな関数 無料で使える中学学習プリント
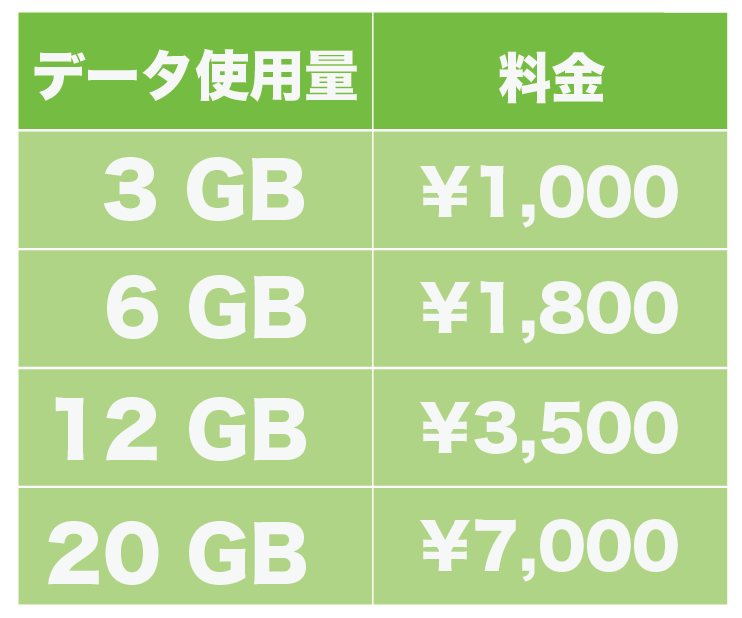



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
1節 いろいろな関数表示の微分法 A 1 ⑴ ② ① 2 2 1 y t x t ①-2×②より x 2y 3 ∴ 2 3 2 1 y x ⑵ ② ① y t t x t 2 2 ①より t x 2 ②に代入し,整理すると y x2 5x 6 ⑶ ② ① y t 1 x tいろいろな関数の微分の説明 に使われています。数学Ⅲの微分積分のテーマは 今まで習った関数の全てを微分(積分)できるようにする ことです。つまり「新しいことがほとんど」 というわけではない ということですね。 もちろん新しいことも出てきます。ですが応用問題の多くは数単元 関数 y = a x 2 (啓林館) 3 いろいろな事象と関数 ・2・ いろいろな関数 全1時間




数学 いろいろな関数の導関数 Youtube
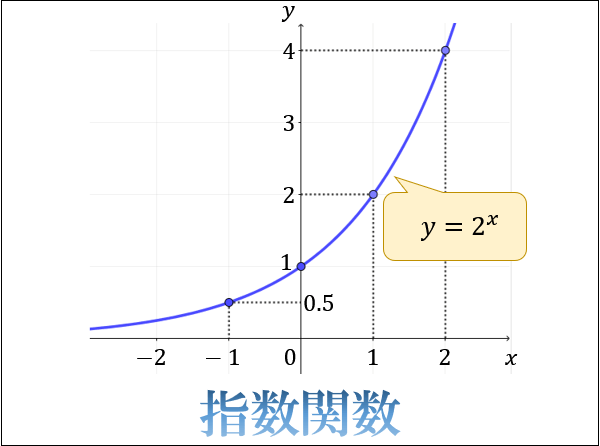



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
いろいろな関数 解説 比例,反比例,1次関数,関数y=ax 2 など,様々な関数のグラフについて学習しました。それらの関数は,xの変域に制限がない場合,ずっとつながったものでしたが,関数のグラフには,ずっとつながっているのではなく,途切れてしまうようなものもあります。身近なIndex関数や、row,column,small,weekday,workdayintlなどなど、いろいろ関数は思いつくのですが、表示結果は月曜日だけ、や水曜日だけ、など、特定の曜日しか表示できなくて困っています。 図のように、横に引っ張ったらその月の複数の曜日から日付を返せるでしょうか? 通報する この質問への回答(1) ガウシアンのフーリエ変換はガウシアン ここで定積分 は次のように 2 次元平面上の積分を使って求められる (2) 指数関数のフーリエ変換はローレンツィアン (3) 正弦波のフーリエ変換はデルタ関数 これは、正弦波が直交基底であるという意味なので天下り的に認める。




麻生雅久の数学なるほど数学iiいろいろな関数 図形と式a Soの解法 試験で点がとれる 大学受験v Books 麻生 雅久 本 通販 Amazon




Limh0dfracsin Xh Sinxh Descubre Como Resolverlo En Qanda
いろいろな 関数 (解説 ) 身の回りには 関数 として 捉える ことのできる 事象 がたくさんある 。その ほとんどが 複雑 なも ので あり 、数式 では 簡単 に表現 できないもの も多い。しかし 中には 比較的 やさ しい 関数 で表す ことのできる 事象 もある基本的な処理でもある総和計算、Pythonだと組み込み関数やNumPyの関数などいろいろ関数で求めることができます。 結局、どれが速いのか?どれを使えばいいのか?知らなかったので、 外出自粛期間の暇つぶしに、比較してみました。 総和計算とは 複数の入力値の合計を求める処理 例いろいろな連続の定義 目次 1 limによる連続関数の定義 逆は必ずしも成り立たないが,区間 \(I\) が閉区間であるとき,連続関数 \(f(x)\) は一様連続となる. 4 \(\varepsilon\delta\) 論法による(距離空間での)連続写像の定義 距離の定義 集合 \(X\) に対して,写像 \(dX \times X




3数 いろいろな関数 Youtube
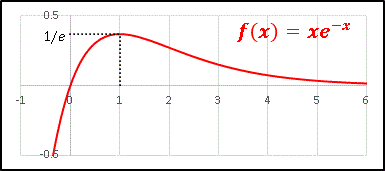



グラフ全体を下に押し下げて平たくなります
いろいろな曲線を方程式の形に表す場合、Y=F(X) のような陽関数だけでは表現しきれ ない。 媒介変数表示の方法は万能ではあるが、式自体に美しさが感じられない。いろいろな関数を作る このレッスンでは、 複数の引数を受け取る関数や 引数に初期値を与える方法など 関数作成のコツを学びます。 引数を受け取って戻り値を返す 関数を作ってみましょう。




高等学校数学ii いろいろな関数 Wikibooks




高等学校数学ii いろいろな関数 Wikibooks



いろいろな関数の積分



指数関数 続き




いろいろな関数




771 三角関数やいろいろな関数で 孤立特異点の値を求め その意味を求める 広い新世界が 広がっている その値を求める明確な意味も 求めている 何でも調べるは 数学の精神ですが 動機や目標 意義は それなりに大事 世には ただ惰性で夢中で やっているは多い



グラフを描くコツ



1
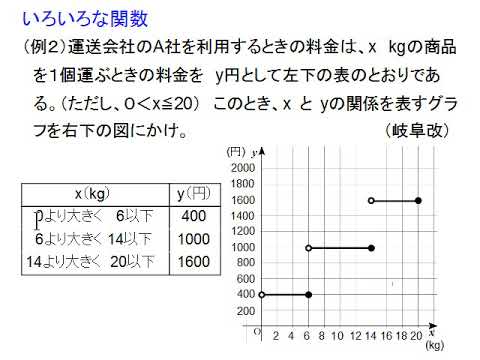



中3数学34 いろいろな関数 Youtube




指数関数をわかりやすく解説 グラフの書き方もマスターしよう 高校生向け受験応援メディア 受験のミカタ




指数関数の定義 なぜ底が負のときは定義しないのか ダルいから 青春マスマティック



Excelでグラフ



世界一わかりやすい数学問題集中3 4章 二次関数




指数関数 対数関数



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




1次不等式 いろいろな関数の問題です F1 数学 箱根駅伝ブログ
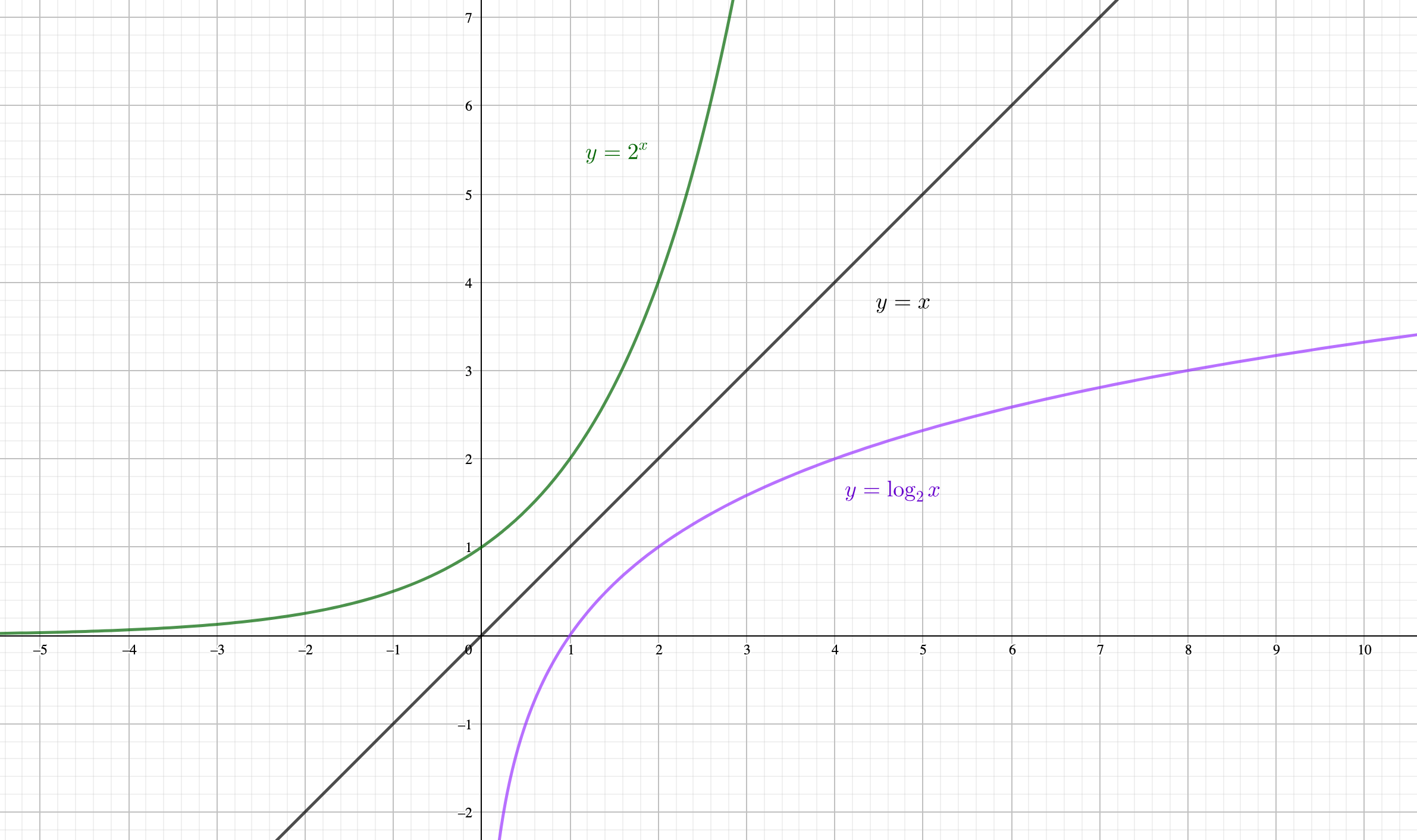



対数関数の定義と性質 グラフからわかる重要性質と問題への使い方を徹底解説 青春マスマティック




高等学校数学ii いろいろな関数 Wikibooks



指数と対数の関係とは 変換公式やグラフの比較 計算問題 受験辞典



数学2基礎 解説 例題コース 三角関数 指数関数 対数関数 最新刊 無料試し読みなら漫画 マンガ 電子書籍のコミックシーモア




中学数学で登場する不連続な関数 身勝手な主張




高等学校数学ii いろいろな関数 Wikibooks



3



指数関数 初等数学 基礎からの数学入門




いろんな関数 高校数学の美しい物語




関数の微分可能性4 指数関数e Xの導関数を微分の定義によって求める 身勝手な主張




高校数学 数 127 指数関数 グラフ編 Youtube




中学生 いろいろな関数の利用のノート一覧 Clear
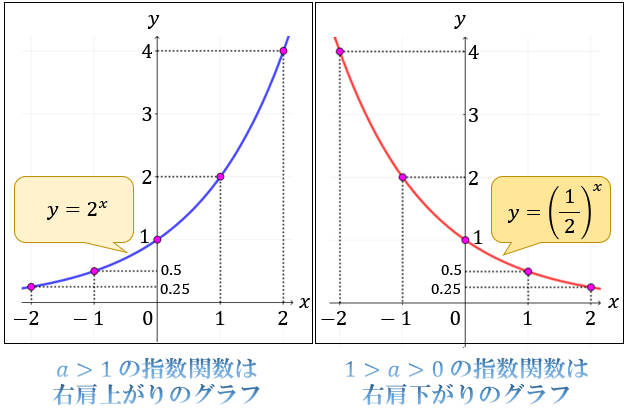



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ



function view問題集 ver3 42j




中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
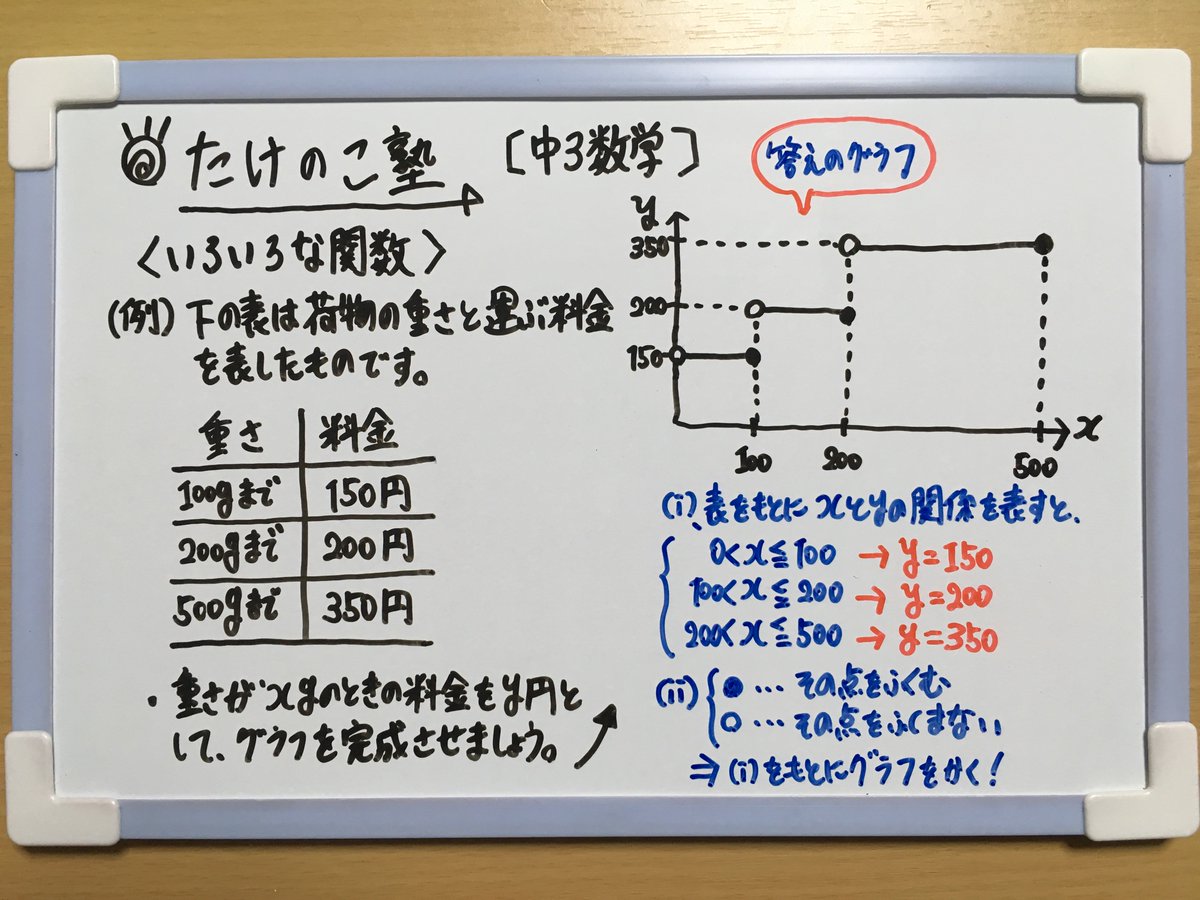



たけのこ塾 Auf Twitter 中3数学 今回は いろいろな関数 を作成しました いろいろな関数のグラフをかくとき はその点をふくむ はその点をふくまないことに注意しましょう 詳しくは画像の解説をご覧下さい 勉強垢 中3 数学 Youtube T




いろいろな関数の導関数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



いろいろな関数




初等関数概説 いろいろな関数 信 一松 本 通販 Amazon
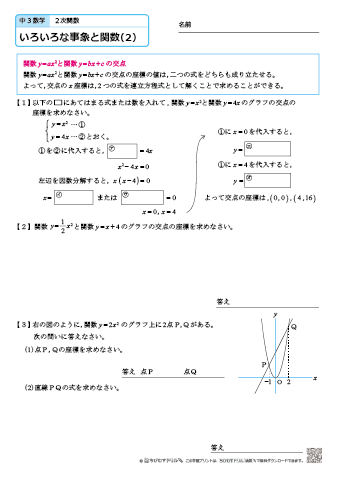



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1
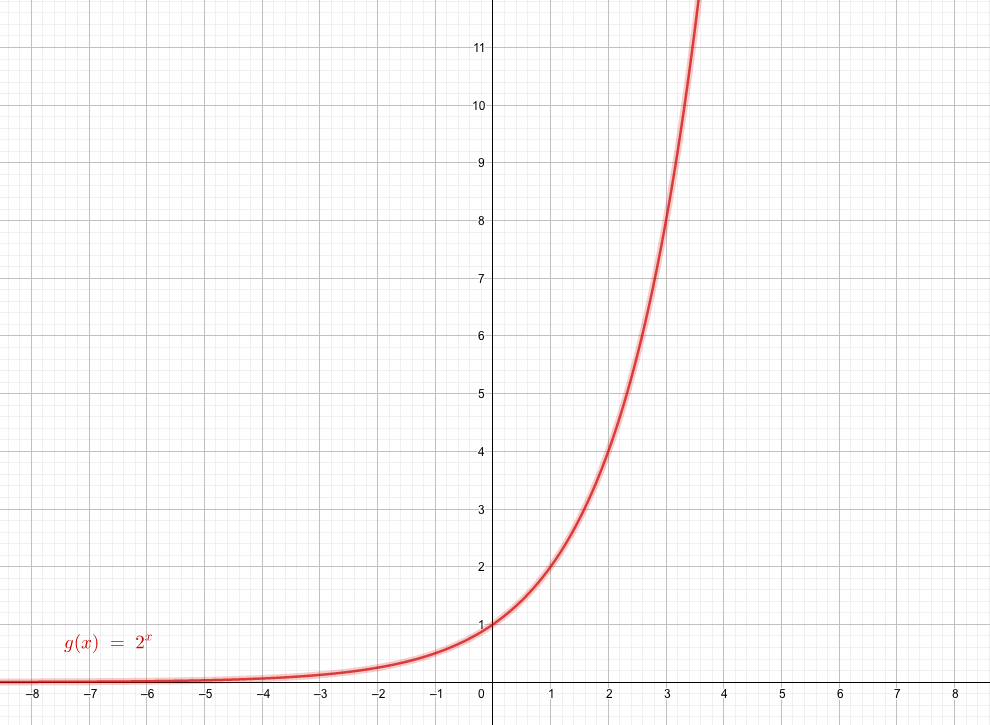



指数関数の定義 なぜ底が負のときは定義しないのか ダルいから 青春マスマティック
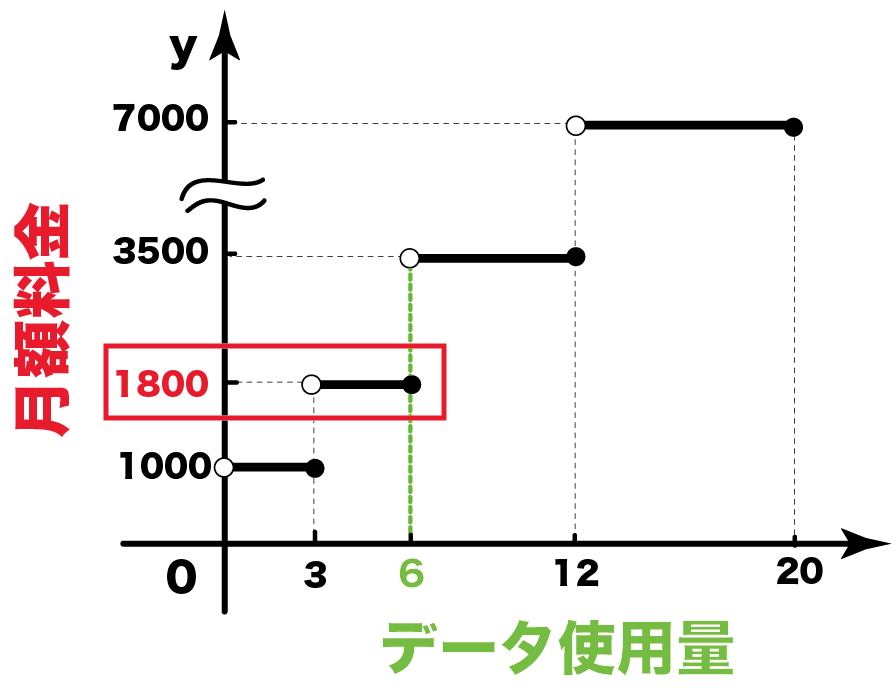



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




ドイツ語で高校数学 いろいろな関数と微分 ふぁそらて 高校生 Note




高校数学7 いろいろな関数 なごみの輪




中3 中3 数学 いろいろな関数の利用 中学生 数学のノート Clear



1




池田洋介の いっきにわかる重要関数 2次関数 三角関数 指数関数 対数関数 数学が面白いほどわかるシリーズ 池田 洋介 本 通販 Amazon



授業実践記録 数学




2 Descubre Como Resolverlo En Qanda




指数関数 Wikipedia



数学2基礎 三角関数 指数関数 対数関数 演習コース 漫画 無料試し読みなら 電子書籍ストア ブックライブ




指数関数的増加 ってどういうこと 秀吉もびっくり 明石の塾なら中谷塾



いろいろな関数の導関数 微分
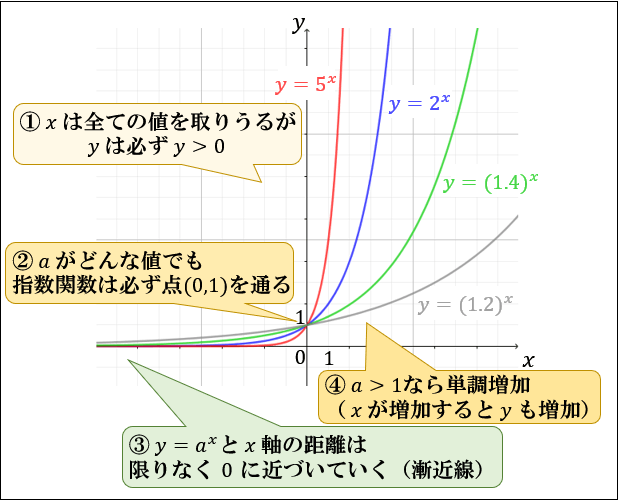



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




高等学校数学ii いろいろな関数 Wikibooks
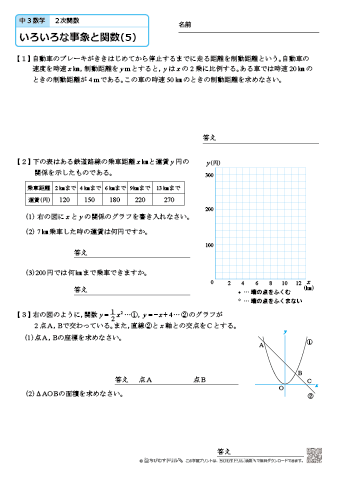



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




関数の単調性の証明 いろいろな方法で示してみよう 身勝手な主張
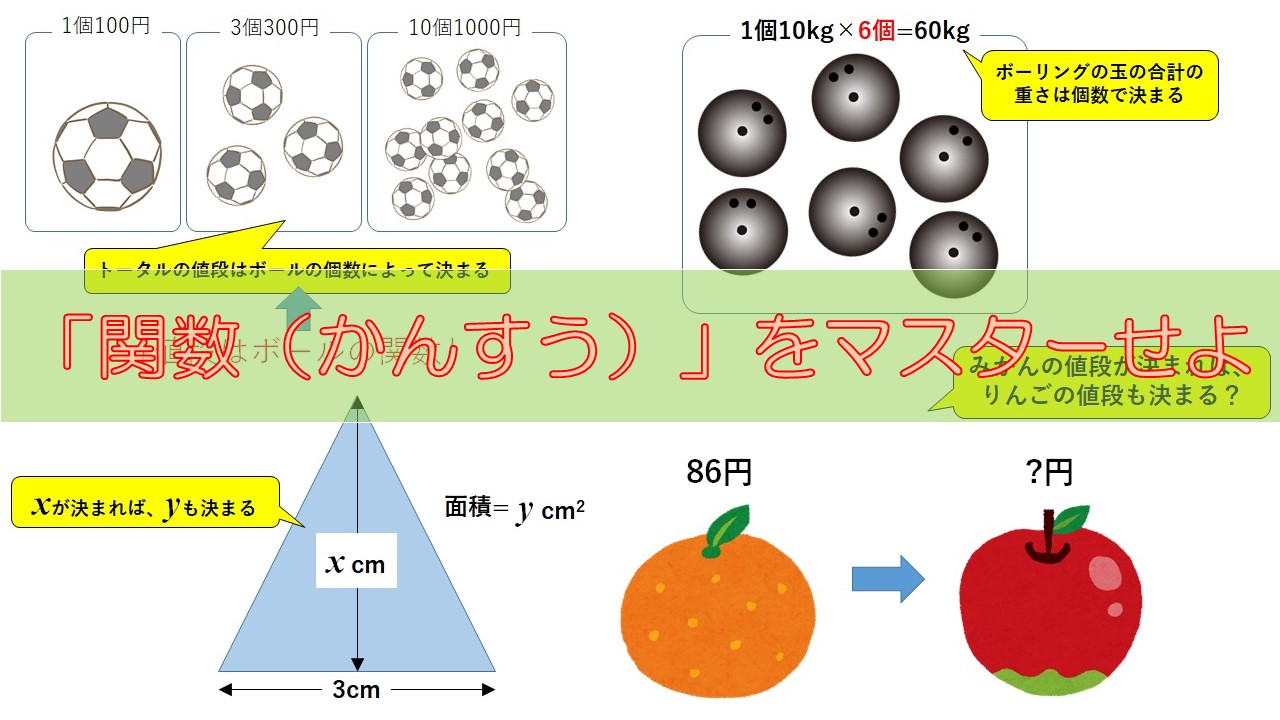



中学1年数学 比例と反比例 関数とは をわかりやすく解説 関数であるもの を選ぶ問題を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト




いろいろな関数 中3数学 関数y Ax二乗 11 Youtube




指数関数的増加 ってどういうこと 秀吉もびっくり 明石の塾なら中谷塾
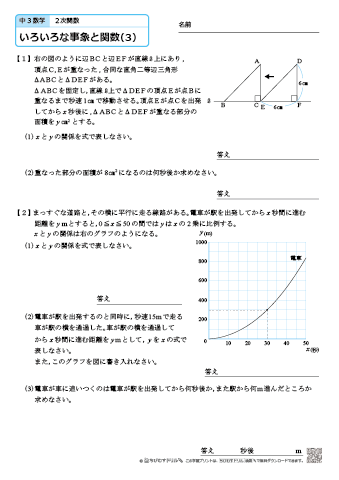



中学3年生 数学 いろいろな事象と関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
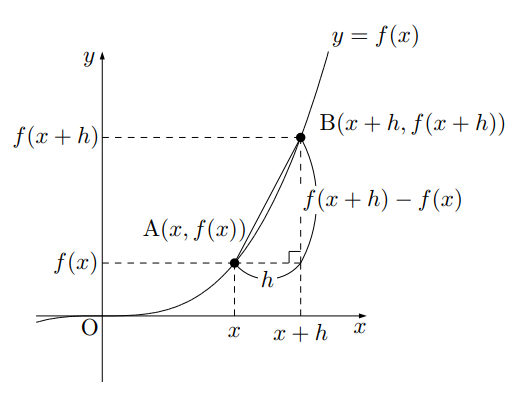



色々な関数の微分 べき関数編 高校数学の知識庫
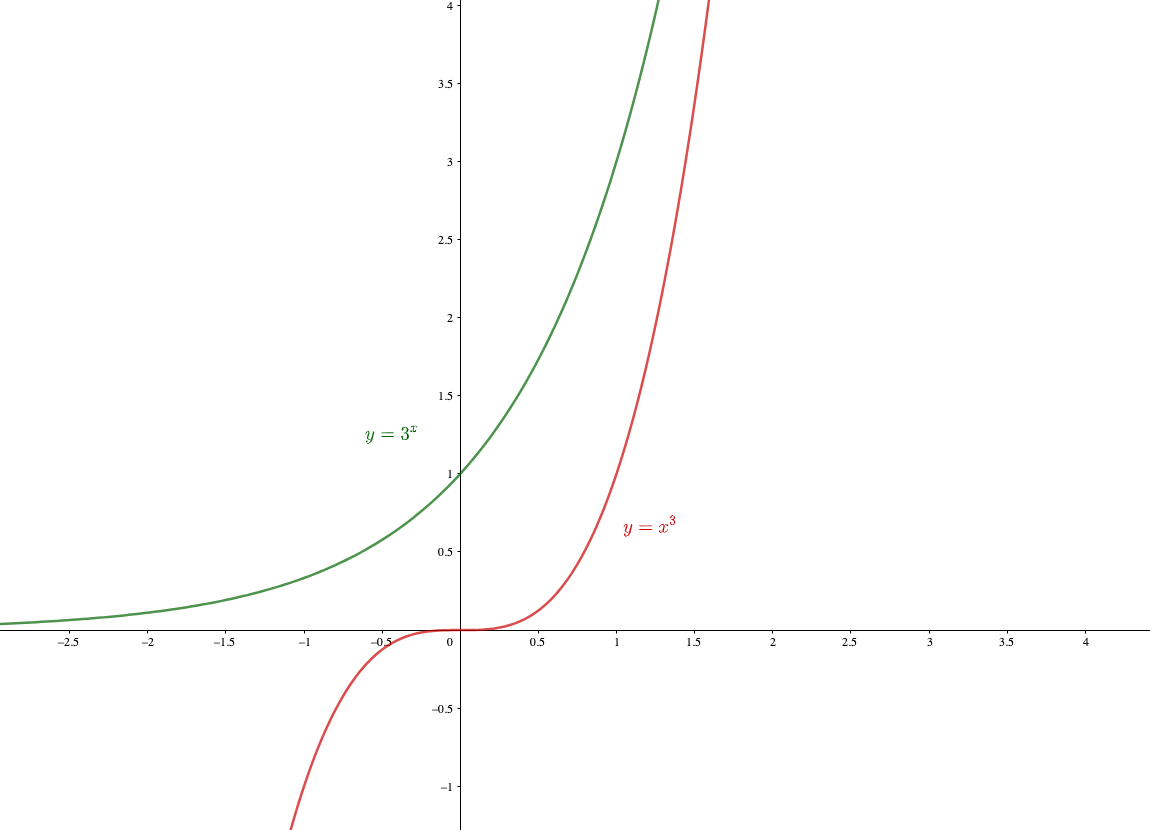



収束 発散の速さ 絶対に覚えておきたい極限の裏公式 見た瞬間に極限がヒラメク 青春マスマティック




いろいろな関数の導関数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



Mathematicaに慣れよう 2
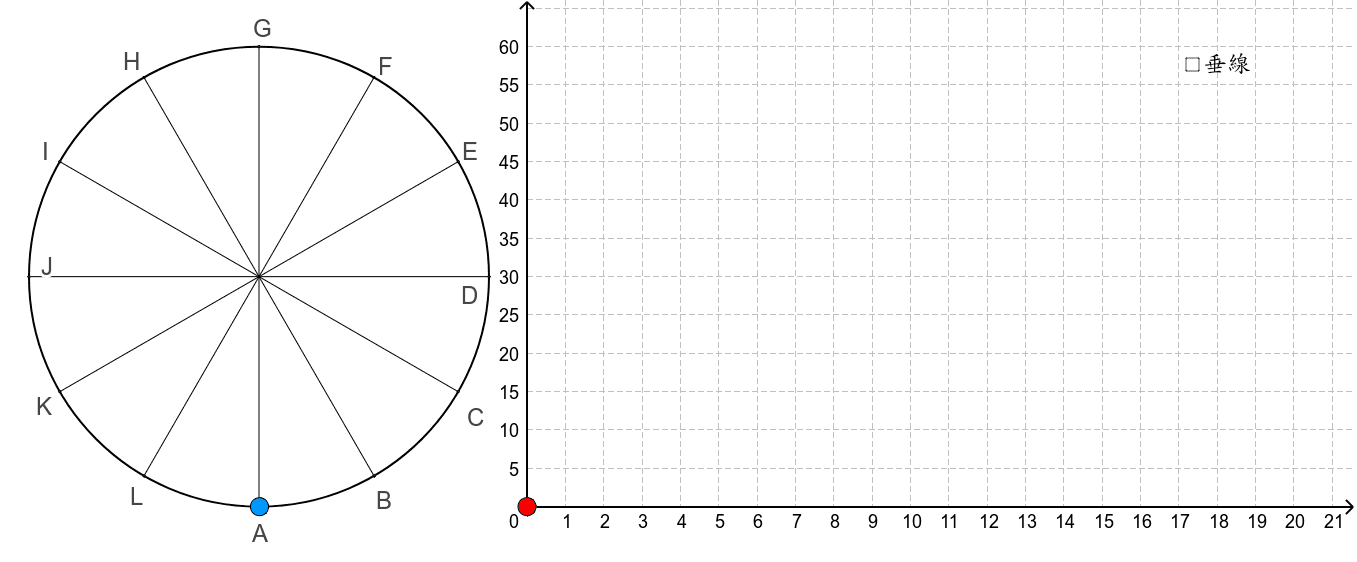



数学3 いろいろな関数 正弦曲線 Geogebra




逆関数とは グラフとその性質 高校数学の知識庫




中学生 いろいろな関数の利用のノート一覧 Clear
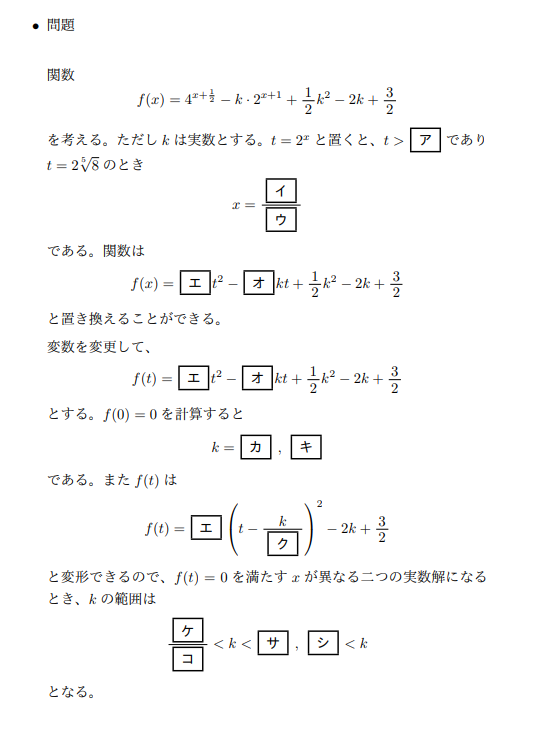



指数関数 対数関数講座その2 指数から二次関数へ 高校数学の知識庫



いろいろな関数 対数
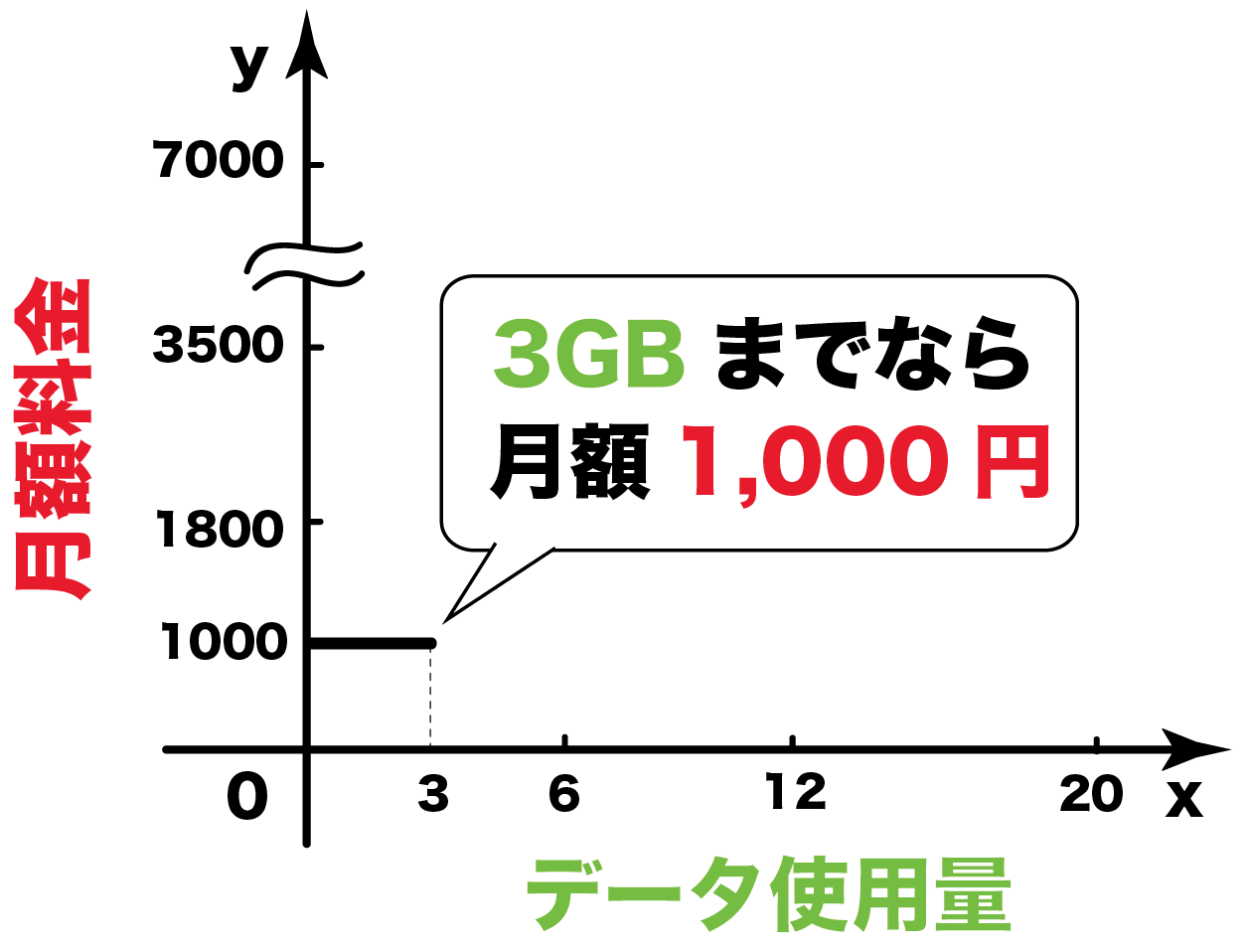



中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




指数関数 対数関数




いろいろな関数のグラフをgoogle先生に教えてもらおう 大学受験プラス




中3 中3 4章 関数y Ax2 2節いろいろな関数の利用 章末 中学生 Clear



複素数の指数関数 対数関数 べき関数




17 9 いろいろな関数 Youtube
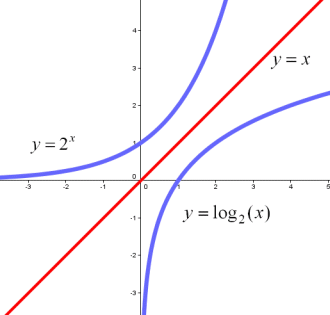



対数 対数関数と指数関数は 逆関数 大人が学び直す数学
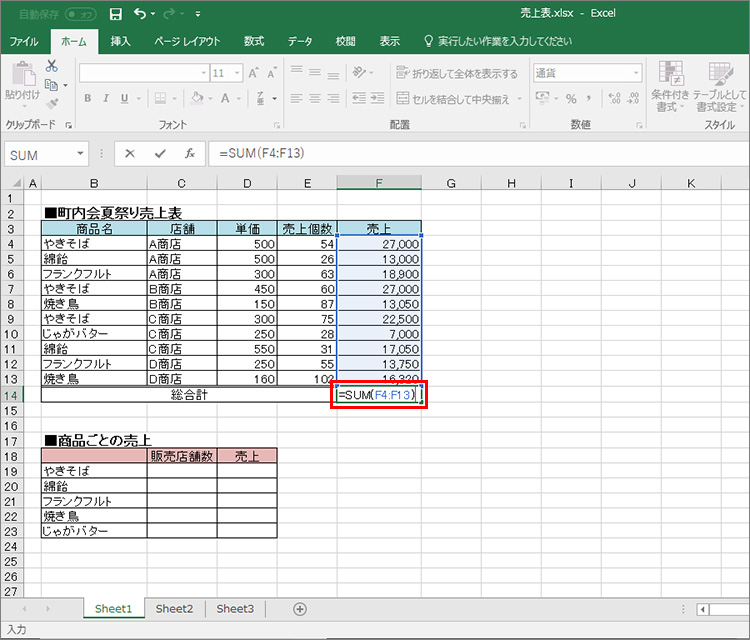



意外とかんたん 9つの関数のワザ エクセル関数特集 Fmvサポート 富士通パソコン



あなたの努力はどちらで報われる 対数的成長か 指数関数的成長か Ichiroyaのブログ




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




関数方程式を考える2 いろいろな関数方程式 身勝手な主張




指数関数の意味と性質 グラフ
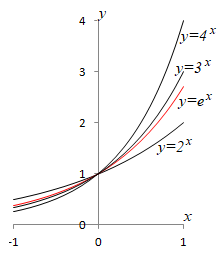



指数関数 対数関数の導関数
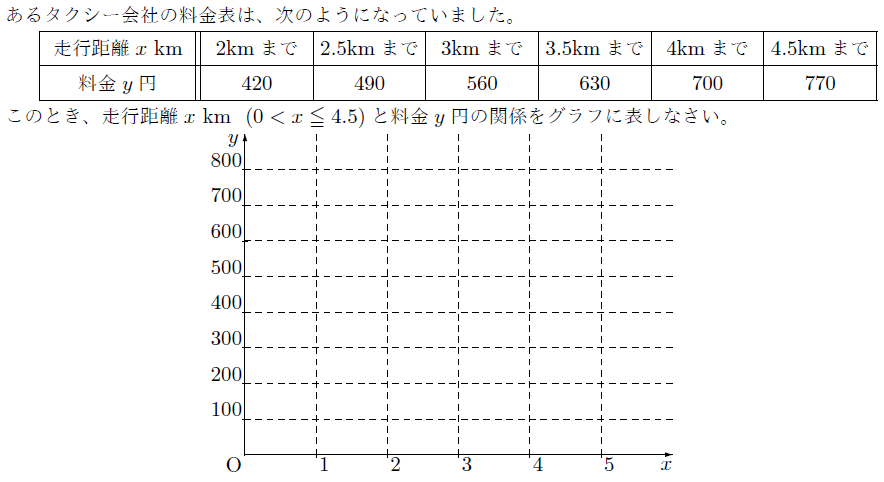



いろいろな関数 まなびの学園




中3数学 いろいろな関数の問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




いろいろな関数の導関数 の問題のわからないを5分で解決 映像授業のtry It トライイット




標準 指数関数の逆関数 なかけんの数学ノート




高等学校数学ii いろいろな関数 Wikibooks




指数関数的減衰 Wikipedia
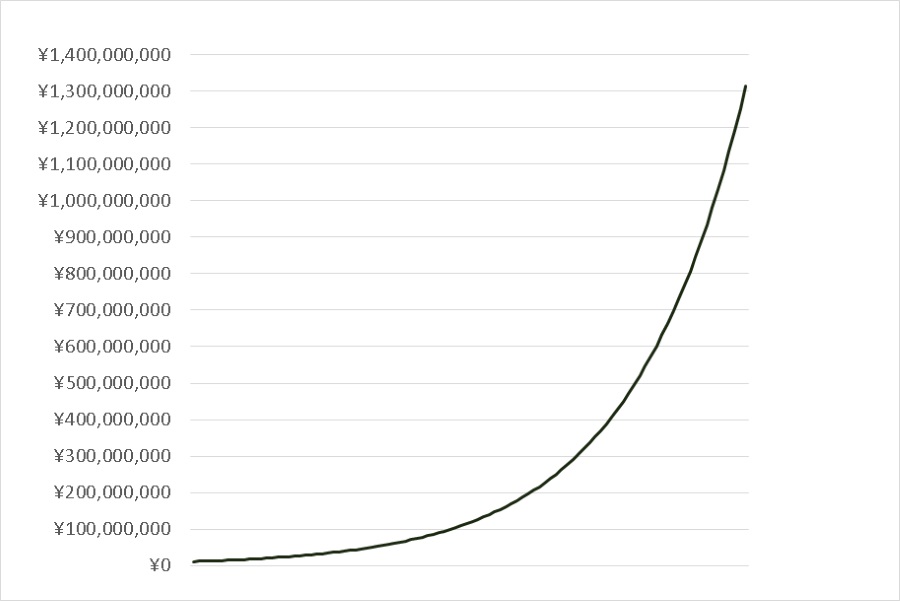



指数法則の一覧 統計学でよく使うもの 統計学が わかった



指数関数 続き




中学2年生の数学です 分からないので解き方教えて下さい Clear



0 件のコメント:
コメントを投稿