学習事項:6章 空間図形 円錐の表面積 ・本時の目標 円錐の側面積の求め方について説明することができる。(思) ・本時の展開 教師の働きかけ( )・予想される生徒の反応( ) 留意点( )・評価(※) 1 問題の把握 次の図 予想しよう。Mixi☆頭の体操☆ 円錐台の表面積は? 図は円錐台(プリン)の展開図です。 表面積を求めなさい。 (ネットより)A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径

公式を図解 すい体の体積 円すいの表面積の求め方
円錐 台 表面積
円錐 台 表面積- 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう! 円錐 台 表面積 底面積は π 9 π c m 2 、側面積は π 15 π c m 2 と計算できるので、ここまでで求めた値を合計すれば表面積になります。 この円錐なら、 ・側面積=$12π cm^2$ ・底面積=$16π cm^2$ なので、合計すると$12
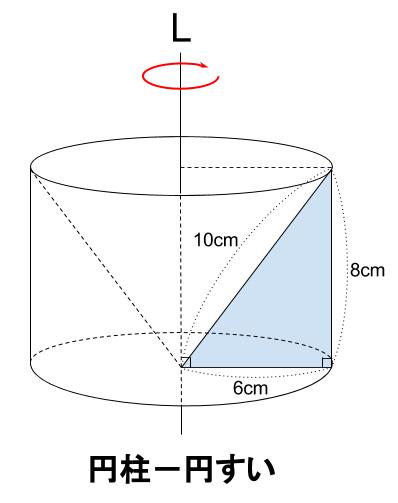



中学数学 回転体 その2 中学数学の無料オンライン学習サイトchu Su
円錐 台 表面積 Search for text in self post contents Suggest as a translation of 占地面積 Here are some resumes of keywords to help you find your search, the copyright owner is the original owner, this blog does not own the copyright of this image or post, but this blog summarizes a selection of keywords you are looking for from some trusted blogs and good i hope this will底面の面積 $\pi a^2$ 天面の面積 $\pi b^2$ 側面積 $\pi(ab)\sqrt{(ab)^2h^2}$ を足し合わせると、円錐台の表面積が求まります。 次回は チェバの定理の覚え方、例題、証明、逆 を解説しま 円錐台の表面積 小学5年生の算数 体積 立体の体積の求め方 練習プリント 円錐台の体積を計算する。『みんなの知識 ちょっと便利帳』の一部です。 円錐台の体積 円錐台の表面積 円錐台の側面積 The site owner hides the web page description 大きな円錐の上側を切り取ったプリンのような図形を円錐台と言います。
側面積=母線×半径×π =9×3×π =27π (㎠) 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積を表面積② 円錐の表面積 円錐の展開図 円錐の場合も、円柱と同じように展開図を書いて考えます。円錐の展開図は、底面の部分の円と、側面の部分のおうぎ形の組み合わせになります。 特に注目するのは、底面の円周(上の図の赤い部分)と、側面のおうぎ形の弧(上の図の緑の部分)は 円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。) 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから
円錐 台 表面積 The site owner hides the web page description Search for text in self post contents Here are some resumes of keywords to help you find your search, the copyright owner is the original owner, this blog does not own the copyright of this image or post, but this blog summarizes a selection of keywords you are looking for from some trusted blogs and good i hope4.補助定理「円錐台の側面積は、S=π(a+b)d で与えられる。」を証明しよう。 5.定理「曲線y=f(x)をx軸のまわりに回転してできる回転体の側面積は、図の中の式で与えられる。」 を証明しよう。 6.問題:球の表面積を求めよう。斜円錐台の高さzhdが与えられて斜円錐の高さzhは与えられない事が多いが比例関係からzh= zhd ah/(ahahs)= zhd/(1ks) と計算出来る。 底面円と小円は相似の関係にあるから小円の寸法は対応する底面円の寸法をks倍すれば求まる。



球の表面積 アルキメデスの方法 4の2 セルフ塾のブログ




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear
No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2立体の体積(V),表面積(S)または側面積(F)および重心位置(G) 角錐台 P12 単位換算 公式計算 平面図形の面積(A),周長(L)および重心位置(G) P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。 参考としてご覧ください。
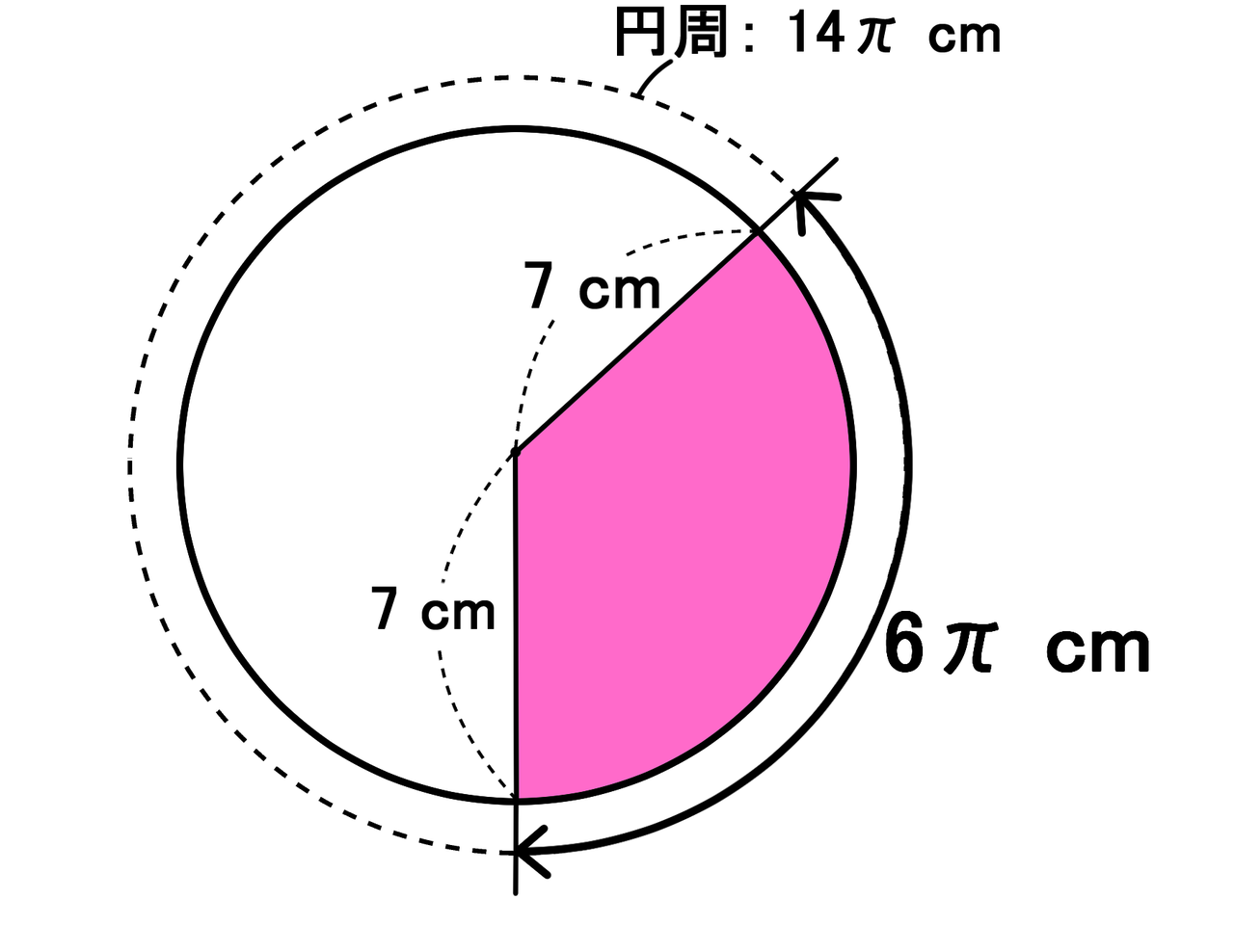



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
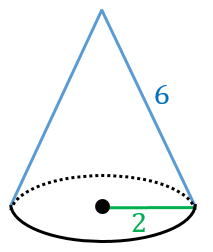



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
「円錐台の体積の求め方は、底面積aの円錐の体積-底面積bの円錐の体積です。 まず、切 以前の ひとこと 19年3月前半 円錐 台 表面積 円錐 台 表面積動画一覧や問題のプリントアウトはこちらをご利用ください。よって、表面積は $15π9π=\textcolor{red}{24π\rm cm^2}$ 母線の長さ 問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐 台 表面積 The site owner hides the web page description 大きな円錐の上側を切り取ったプリンのような図形を円錐台と言います。




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐台の公式 体積 面積 数学 エクセルマニア
円錐台の体積 110 /138件 表示件数 5 10 30 50 100 0 1 1632 男 / 歳未満 / 会社員・公務員 / 非常に役に立った / 使用目的 拡底杭の拡底部の計算 ご意見・ご感想 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。円錐の側面積は3つのステップでもとめることができるよ。 つぎの例題をといていこう! 例題 四角錐台の体積 高精度計算サイト 底面の面積 $\pi a^2$ 天面の面積 $\pi b^2$ 側面積 $\pi(ab)\sqrt{(ab)^2h^2}$ を足し合わせると、円錐台の表面積が求まります。 円錐台の側面積 円錐の側面積はπ× (底面の半径)× (母線の長さ)で表されることを用います (詳細: 直円錐の側面を展開した扇形の中心角)。 "大きな"円錐の母線の長さは a√ { (ab)2h2}/ (ab) 、"小さな"円錐の母線の長さは b√ { (ab)2h2}/ (ab) なので、円錐台の側面積Fは以下のようにな




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
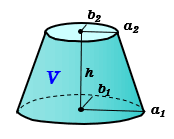



楕円錐台の体積 高精度計算サイト
ところで有り難いことに,皮巾は太くても細くても円錐台の高さの和がrでありさえすれば表面積は円柱の側面積2πr に等しいんだから,半球の表面積は2πr だ.極端な場合はθ= のときの円錐下半分の側面積に等しい.これは円錐の側面積の だから相似比 で縮小した円錐:半球と底面を共有し 円錐 台 表面積 円錐 台 表面積円錐台の表面積 底面の面積 $\pi a^2$ 天面の面積 $\pi b^2$ 側面積 $\pi(ab)\sqrt{(ab)^2h^2}$ を足し合わせると、円錐台の表面積が求まります。 次回は チェバの定理の覚え方、例題、証明、逆 を解説します。V=容積、S=表面積、As=側面積、Ab=底面積、χ=底面より重心までの距離 截頭円垂 角 垂 球 欠 球




実用数学技能検定 数検 おはようございmath 今日は10月25日 毎日25日は プリンの日 だそうです 一般的にプリンの形は 円錐台ですね ということで プリンの表面積と体積を計算するための公式をお伝えしますね 実際に計ってみてください プリン
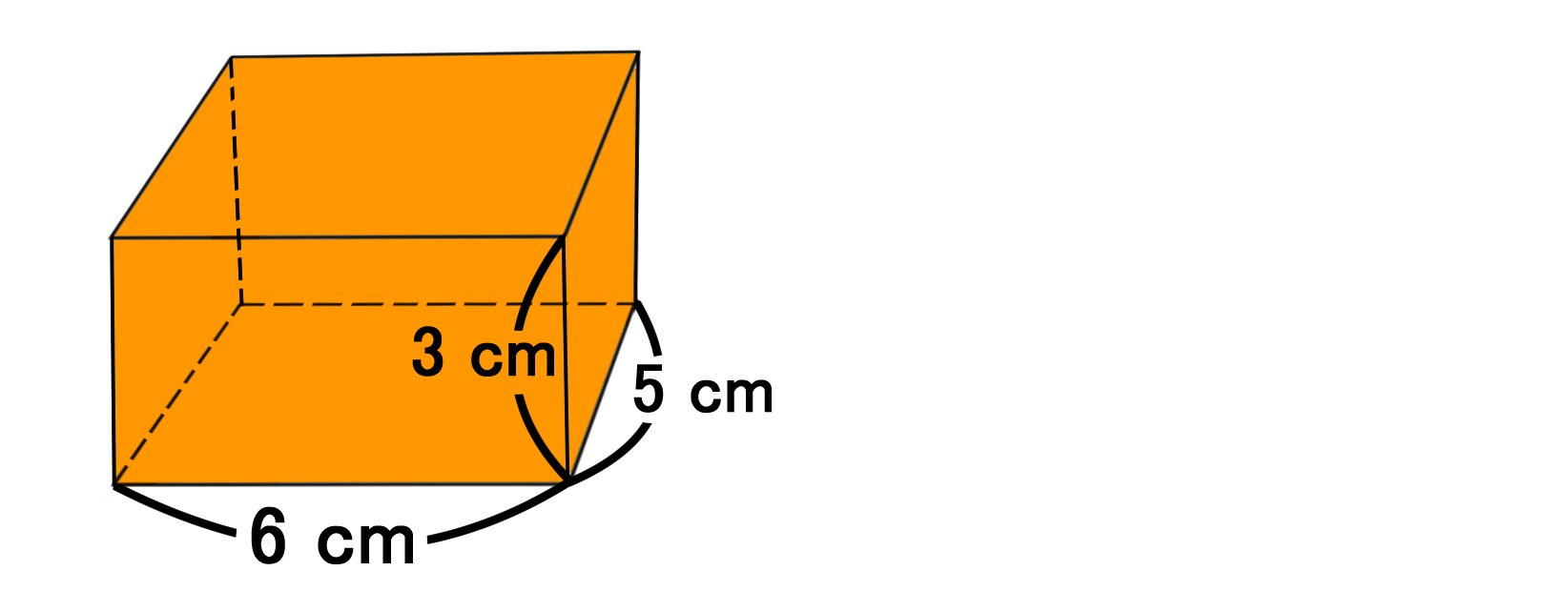



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S 円錐 円錐(えんすい,英 cone)とは,円を底面として持つ錐(きり)状にとがった立体のことである‥. Wikipedia先生によると円錐とはこのような立体のことらしいです. 今日は円錐についてのブログです. 表面積を求める公式 S = r π (r m) S = r π (r m) 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。
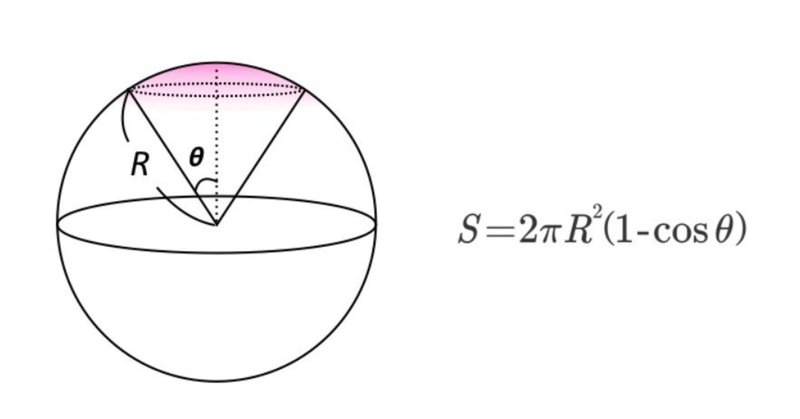



28で見込む部分の球の表面積の計算 Matsubayashi Note




年度 立教新座高校入学試験を解いてみた 4 Seraph Boy 渦巻く記憶 小学生当時 偏差値30代のライトノベル作家が入試問題を解くと



添付写真の図形の展開図が知りたいです 仕事の依頼でこちらの図形の Yahoo 知恵袋




円錐 展開図 書き方 円錐 作図 ハロウィン かぼちゃ イラスト
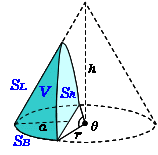



一部が欠けた直円錐の体積 高精度計算サイト




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Q Tbn And9gcqjobggcmt23 2z3kno11yv3jyxklvrxkobpwlhwovwikso5zii Usqp Cau




初等幾何 球の表面積を求める 大人が学び直す数学




2014年大学入試問題より3 一橋大学 円錐の表面積に関する問題 身勝手な主張




ダウンロード 円錐 台 表面積 ドラえもんの壁紙




円錐の表面積の求め方 公式と計算例



Toukou27
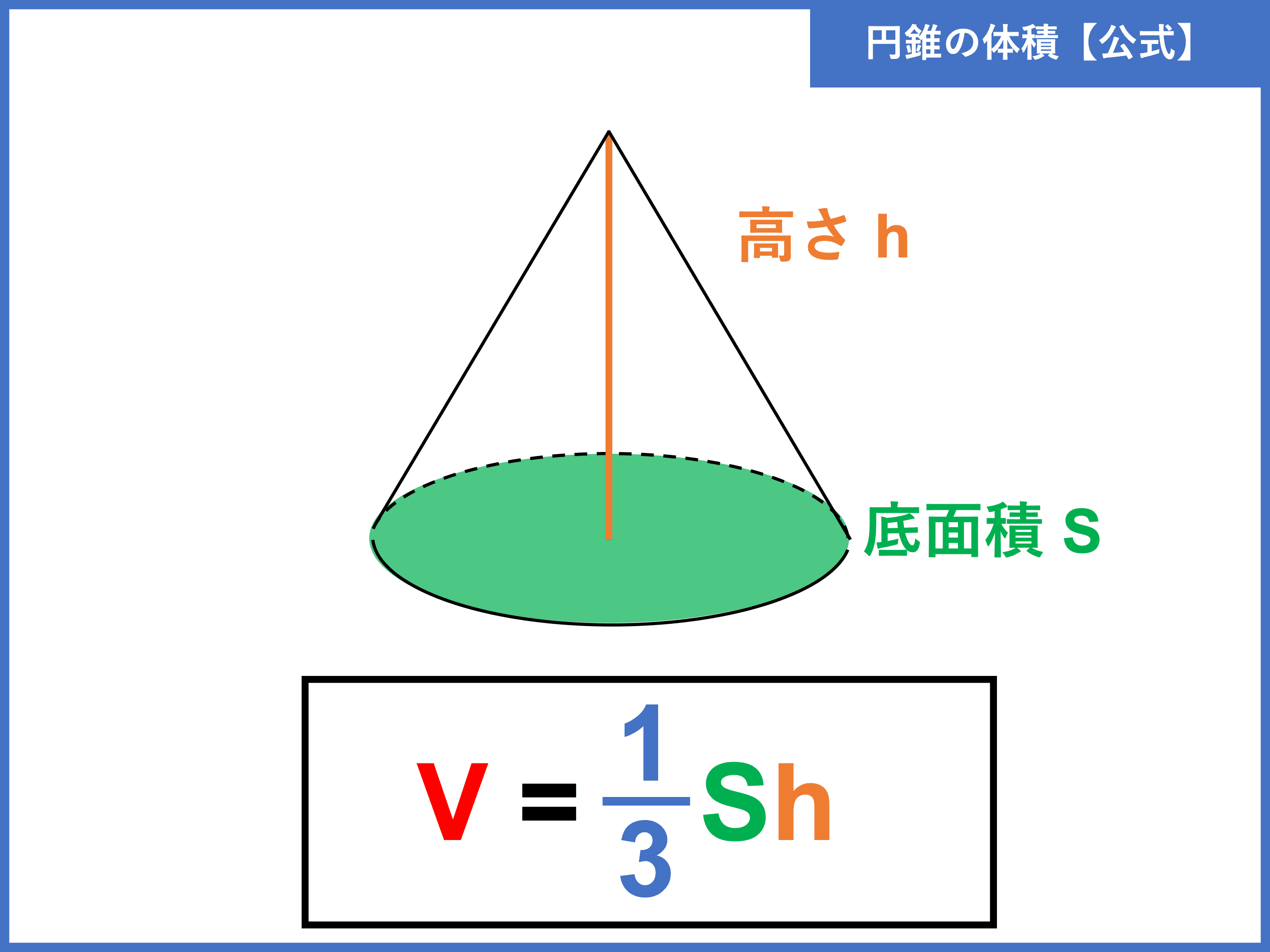



Hd限定円錐 体積 の 求め 方 ページを着色するだけ
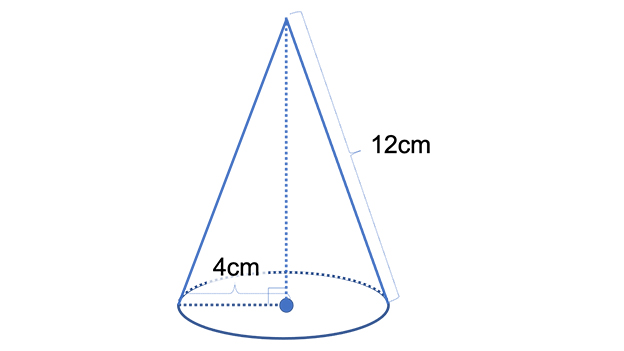



表面積 の求め方まとめ 立体ごとの違いやポイントをチェック お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




公式を図解 すい体の体積 円すいの表面積の求め方




表面積の求め方 計算公式一覧




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




公式を図解 すい体の体積 円すいの表面積の求め方




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



この円錐台の表面積の答えは210pなのですが 大きい円錐から小さい円錐を引い Yahoo 知恵袋




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
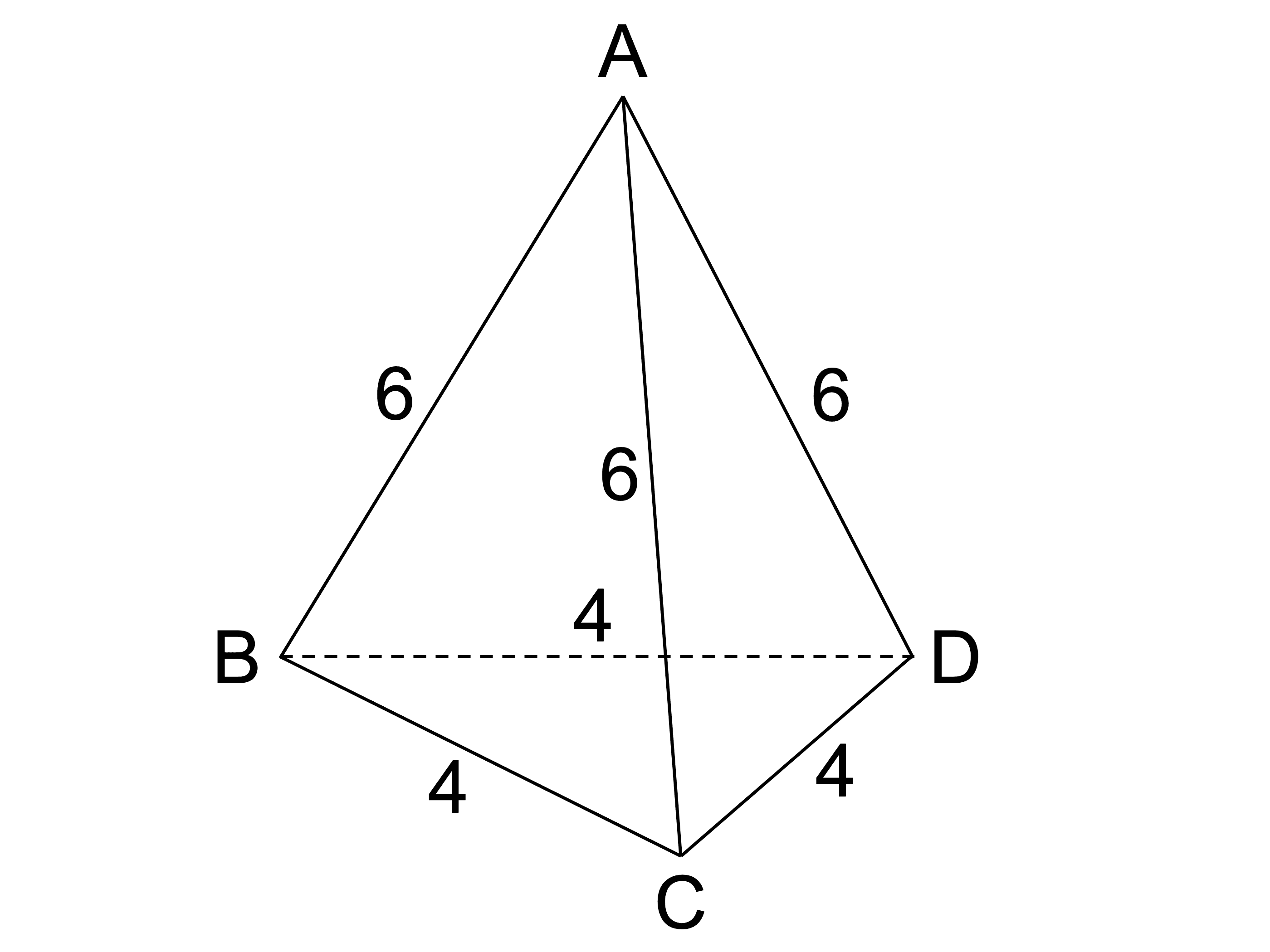



50 グレア 三角錐 展開図 書き方




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su



中三です 今日の数学で 円錐の相似比 体積比などを教わりました Yahoo 知恵袋




中学数学 回転体 その2 中学数学の無料オンライン学習サイトchu Su




円錐の体積ってなんであの公式なの Webty Staff Blog




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




直円錐の側面を展開した扇形の中心角 香料ゐっすゐの夢
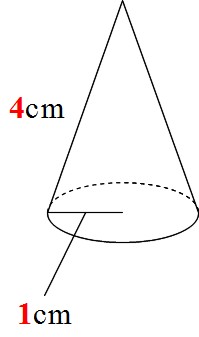



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
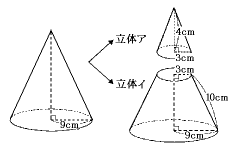



吉祥女子中学校入試問題のポイント
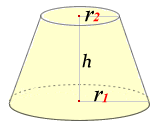



みんなの知識 ちょっと便利帳 円錐台の側面積を計算する
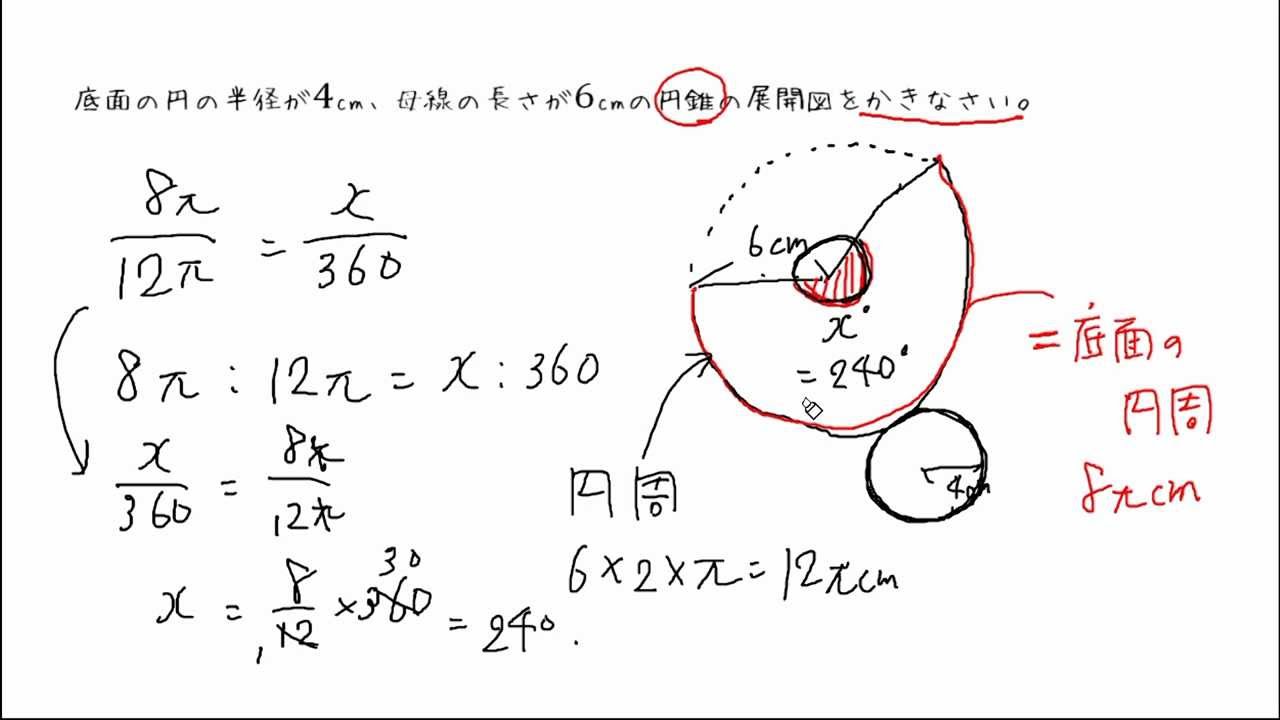



円錐の展開図 Youtube




円錐の体積ってなんであの公式なの Webty Staff Blog



Newみんなの算数講座104 プリン 中学受験の算数知恵宝庫




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



円すい台側面積の公式を導く




円錐の表面積の求め方 公式と計算例
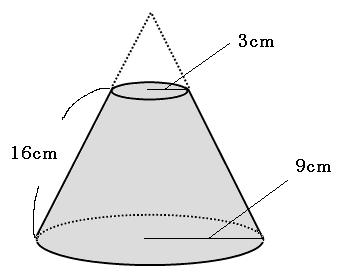



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



私立中学 入試 問題の難問 偶然に 正解 セルフ塾のブログ
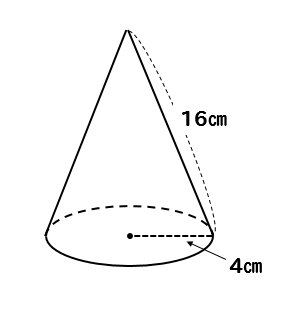



円錐を転がすと1周するのにどれくらい回転する 入試問題を解説 数スタ
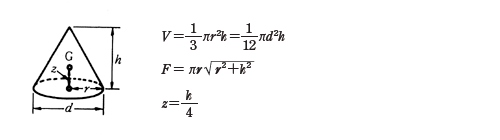



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円錐 P12




表面積の求め方 計算公式一覧



円錐台の表面積の問題です 大きい円錐の表面積 小さい円錐の表面積 小 Yahoo 知恵袋




公式を図解 すい体の体積 円すいの表面積の求め方



1




算数図形編 円柱 円すい 展開図 切断 円すいが切り取られた形は相似を使おう 中学受験 高校受験パスナビ
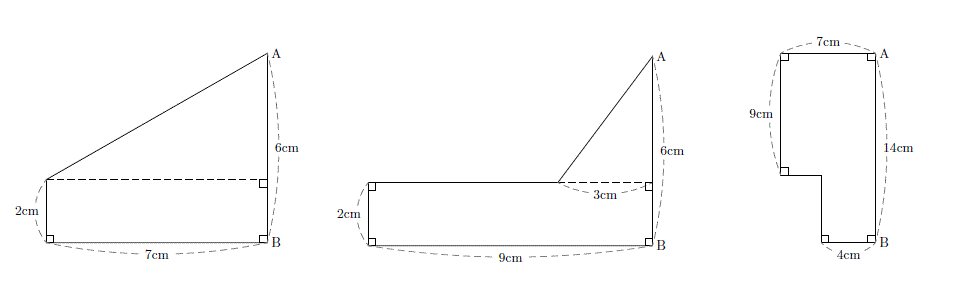



かみのドリル 立体の体積と表面積 回転




円錐台 Wikipedia



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
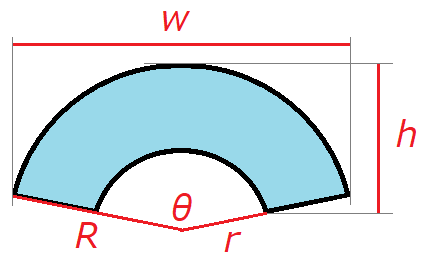



漏斗 円錐台 の立体形状から平面の展開図 扇形環 を得る 高精度計算サイト
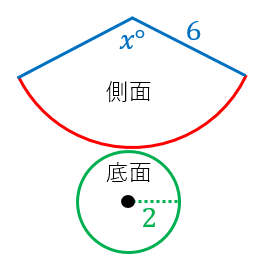



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




表面積の求め方 計算公式一覧
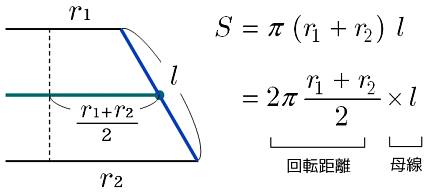



初等幾何 円錐台の側面積を求める 大人が学び直す数学



1




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear




相似比と体積比 円錐台 中学3年数学 Youtube



Math 円錐 円錐台と面積比 体積比 働きアリ



Math 回転体の体積 表面積とパップス ギュルダンの定理 働きアリ The 2nd
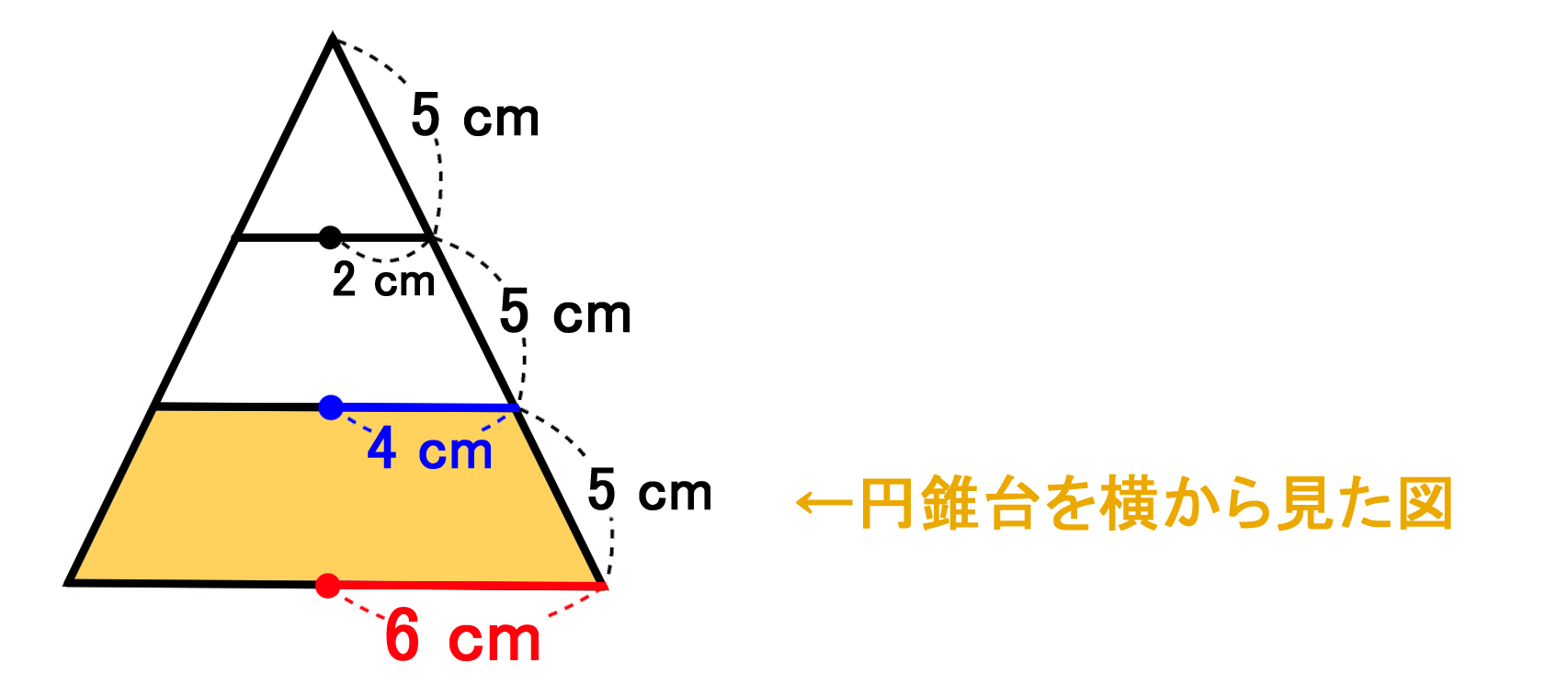



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




入力数値についての説明図 ペーパーモデル 円錐 メモ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




円錐 展開図 ダウンロード ダウンロード に際しましては あらかじめ免責事項をご確認ください 全学年共通 立体の展開図 円錐




円錐台の体積 側面積 香料ゐっすゐの夢




円錐の表面積 Youtube




中1数学 空間図形 勉強 Youtube スタディチューブ




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




四角錐台の体積 高精度計算サイト




空間図形14 円すい台の体積 Youtube




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
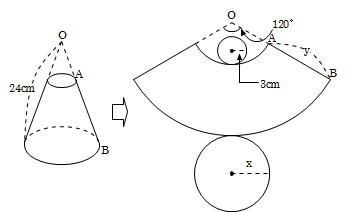



小5の学習ポイント5 すい体と回転体 前田昌宏の中学受験が楽しくなる算数塾




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




年度 立教新座高校入学試験を解いてみた 4 Seraph Boy 渦巻く記憶 小学生当時 偏差値30代のライトノベル作家が入試問題を解くと




円錐台の問題がわかりません 写真は円錐の上部を底面に平行な平面で切った円 Okwave




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
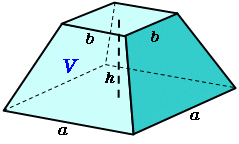



正四角錐台の体積 高精度計算サイト
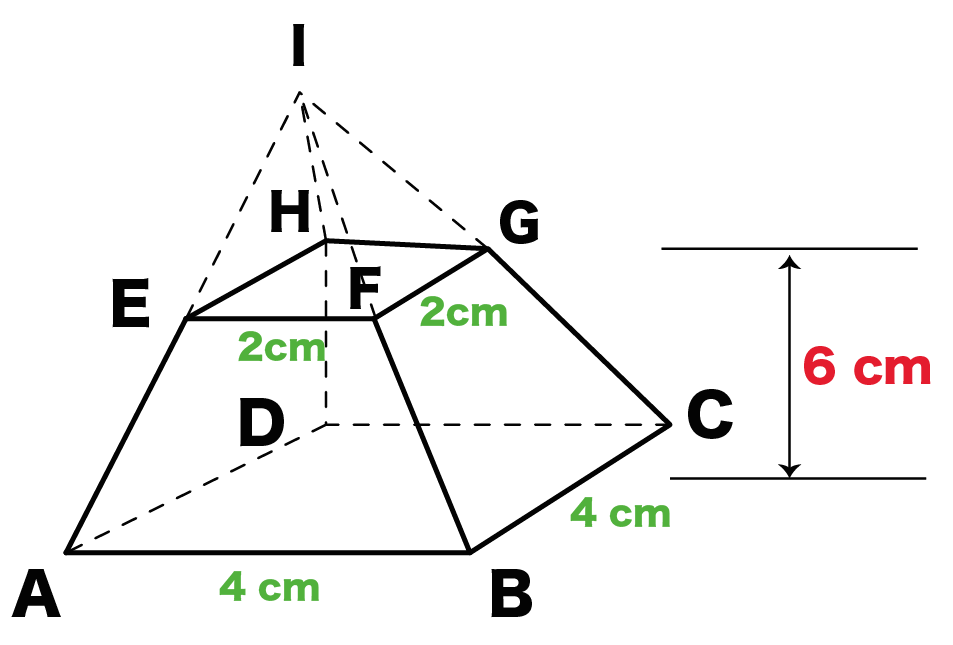



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直円錐を平面で切ったとき 分断される部分の体積と表面積 特殊相対性理論 電磁気学 数学



1
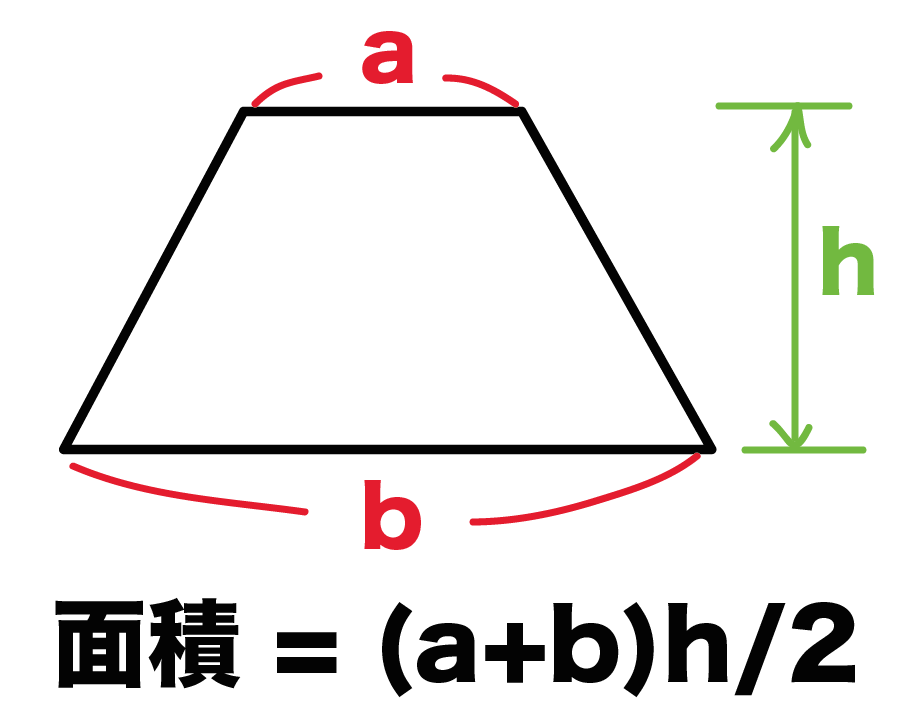



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear
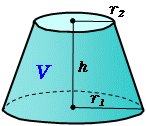



円錐台の体積 高精度計算サイト



円錐を高さ4分の1だけ切り取ったものである この円錐台の側面積を求めよ 回 Yahoo 知恵袋
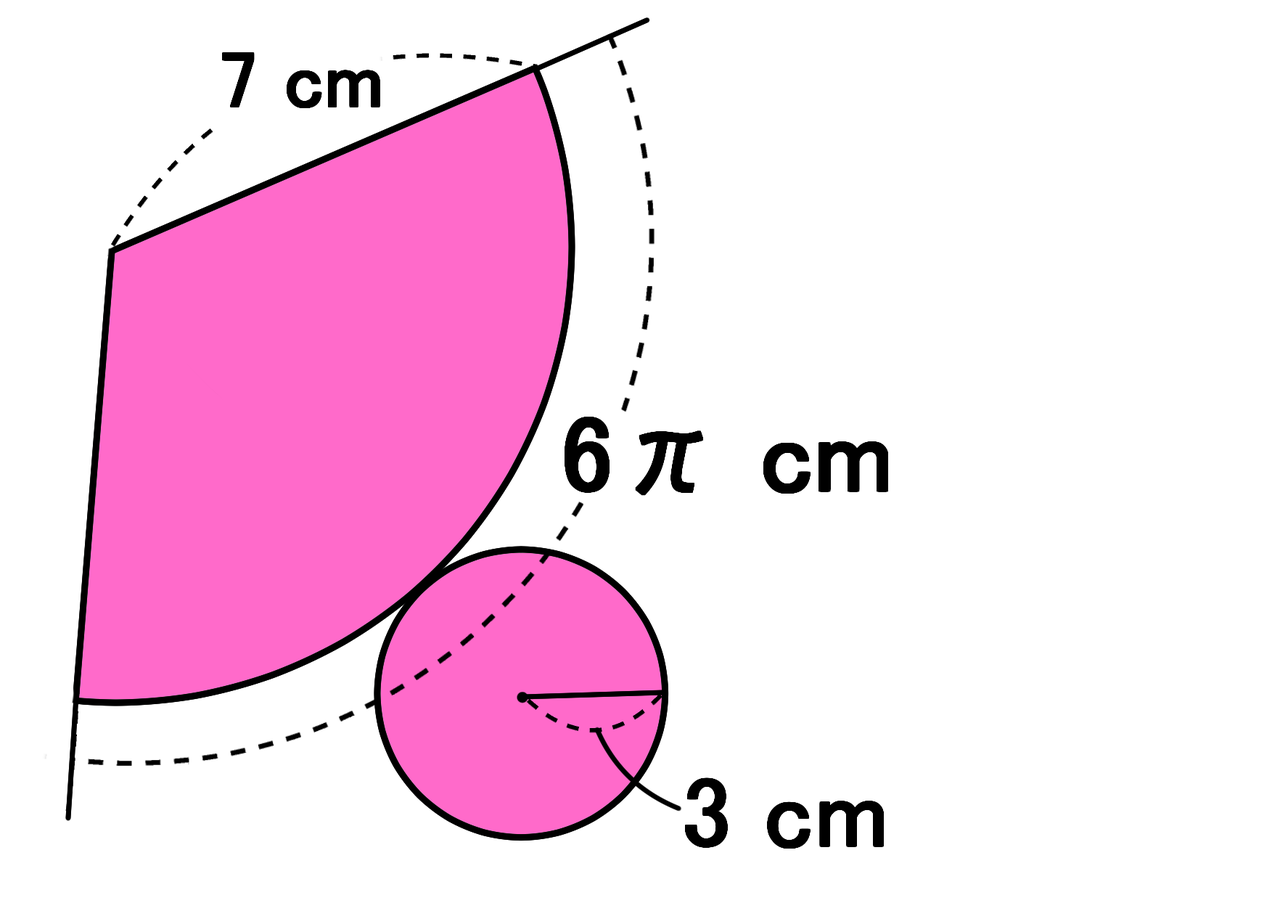



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
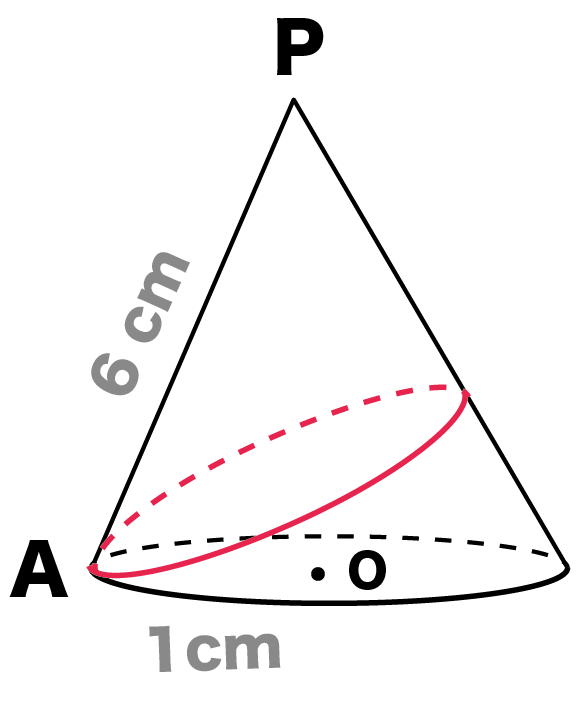



円錐にかけたひもの最短距離を求める3ステップ Qikeru 学びを楽しくわかりやすく




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく



楕円 錐 展開 図



0 件のコメント:
コメントを投稿