If y = 1 1/x 1/x 2 1/x 3 ∞ with x>1, then dy/dx is equal to If y = 2 log x , then dy/dx is equal to If y = 4x – 5 is tangent to the curve y 2 = px 3 q at (2, 3), thenY=log (x2/e2) diff wr to x , we get dy/dx=1/ (x2/e2) (2x/e2) =2/x diff wr to x again d2y/dx2=2/x2 Thanks & RegardsGet an answer for '`y = x^(2/x)` Use logarithmic differentiation to find dy/dx' and find homework help for other Math questions at eNotes
What Will Be The Value Of D Dx Log 1 X 2 Quora
Y=log(1-x^2/1 x^2) find dy/dx
Y=log(1-x^2/1 x^2) find dy/dx-Sketch a few solutions of the differential equation on the slope field and then find the general solution analyticallyWeekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled




Hi My Question Is If Y Log X 1 X 2 1 2 2 Find Dy Dx And D 2y Dx 2 Maths Continuity And Differentiability Meritnation Com
Taking logarithm of both sides, we get log y = `log (1 1/"x")^"x"` ∴ log y = x `log (1 1/"x")` Differentiating both sides wrtx, we get `1/"y" * "dy"/"dx" = "x" * "d"/"dx" log (1 1/"x") log (1 1/"x") * "d"/"dx" ("x")`Y = logx x2 a2 y1 = dxdy = x x2 a2 1 (1 2 x2 a2 2x )y1 = x x2 a2 1 ( x2 a2 x2 a2 x )⇒ y1 ( x2 a2 ) =1Again differentiate,⇒ y2 ( x2 a2 ) 2 x2 a2 12xy1 = 0⇒ y2 (x2 a2)xy1 = 0Answer to Solve the initial value problem dy/dx = (y^2 1)/(x^2 1), y(2) = 2 By signing up, you'll get thousands of stepbystep solutions to
Ex 96, 7 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑥𝑙𝑜𝑔𝑥 𝑑𝑦/𝑑𝑥𝑦=2/𝑥 𝑙𝑜𝑔𝑥 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q xlog x 𝑑𝑦/𝑑𝑥 y = 2/𝑥 log x Dividing by x log x, 𝑑𝑦/𝑑𝑥𝑦" × " 1/(𝑥 log𝑥 ) = 2/𝑥 𝑙𝑜𝑔 𝑥" × " 1/(𝑥 log𝑥 ) 𝑑𝑦/𝑑𝑥 If x = sin(\(\frac{1}{a}\)log y) , show that (1–x2)y2–xy1–a2 y = 0 Note y 2 represents second order derivative ie \(\frac{d^2y}{dx^2}\) and y 1 = dy/dx Given, x = sin(\(\frac{1}{a}\) log y) \((logy)=asin^{1}x\) y = \(e^{asin^{1}x}\)equation 1 to prove (1 x 2)y 2xy 1 a 2 =0 We notice a second–order derivative in the expression to be proved so first take the step to Delta2 said No it doesn't matter where you put the constant neither if you set it equal to or , because given an initial condition you will get the same formula for v in both cases, but the exact value of the constants will be different (for example if you find k=2 for the one case, you ll find k=1/2 for the other case) nice delta Jul 1
Compute $$\iiint\frac{xz}{1x^2y^2}\,dz\,dy\,dx,$$ where $1≤x^2y^2≤3, 0≤z≤3$ I've tried it But I'm only confused with $\theta$ I think it should be $0$ to $2\pi$, but that'll make the whole value zero We have to solve this by the cylindrical method Without solving for theta I get $\frac{9}{2{(π/6)4}}$ As log(xy)=x^2y^2 or logxlogy=x^2y^2 assuming base is e, we have on differentiation 1/x1/y(dy)/(dx)=2x2y(dy)/(dx) or (dy)/(dx)(2y1/y)=1/x2x or (dy)/(dx)=(1/x2x)/(2y1/y)=(y2x^2y)/(2xy^2x) In case base is 10, we can write it as lnx/ln10lny/ln10=x^2y^2 and differentiating gives us 1/ln10(1/x1/y(dy)/(dx))=2x2y(dy)/(dx) or (dy)/(dx)(2yln101/y)=2xln101/x or (dy)/(dx)=(2xln101/x)/(2yln101/y)=(y2x^2yln10)/(2xy^2ln10x)Y = log(x 1/x) y = log((x^21)/x) y = log(x^21) log x Now, you have to recall the derivative formula for logarithmThat is, log y = 1/y * dy




Find Dy Dx When Y E Xlog 1 X 2




If Y Log 1 Sqrtx 1 Sqrtx Then Dy Dx
Answer to Find dy/dx for the following y = (1 x)/(1 x) By signing up, you'll get thousands of stepbystep solutions to your homework If y = e a cos1 x , 1 Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve such problems




Engineering Mathematics Notes




If Y Log 1 X 2 1 X 2 Then Find Dy Dx Maths Meritnation Com
Answer to dy 24(2 5)2 dy O Find da , where da ( 3) (ac 5) 3 dy (ac 5) 2 O y dx (x 3)2 (a 3)3 dy 24(x 5)2 O dx (2 3) 4 dy 1 O dx (x 3)6 8 The given differential equation is solved using the following steps (i) Take natural logaritm on both sides and then simplify the obtained equation using the properties of logaritm I was going through past papers of ODEs course I came across a question solve $$\frac{dy}{dx} = \frac{1}{xy^2},\qquad y(2) = 0$$ I have no clue how to proceed I have suspicion that this equation has no closed form solution and may be there was a mistake in the question Course is a basic course on ODEsGet 11 help now from expert Calculus tutors Solve it with our calculus problem solver and calculator COMPANY About Chegg



If Y Log Tan X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community



Ipvg28rwi2wcwm
Y = log {x√ (1x)} dy/dx = 1/ {x√ (1x^2)} 1 {1/2√ (1x^2)}2x dy/dx = 1/ {x√ (1x^2)} 1 x/√ (1x^2) dy/dx = 1/ {x√ (1x^2)} {√ (1x^2) x }/√ (1x^2) dy/dx = 1/√ (1x^2) , Answer 13K viewsBernoulli's equation has form, \frac{dy}{dx}p(x)y=q(x)y^n Now, consider this, \frac{dz}{dx}z^2x=z^2z This easily simplifies to, \frac{dz}{dx}z=(1x^2)z^2 where p(x)=1 Bernoulli's equation has form, d x d y p ( x ) y = q ( x ) y n Now, consider this, d x d z z 2 x = z 2 z This easily simplifies to, d x d z − z = ( 1 − x 2 ) z 2 where p ( x ) = − 1Click here👆to get an answer to your question ️ If y = log7 (log x) find dydx Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Derivative of Exponential and Logarithmic Functions Let y = e x 1 then find d x 2 d 2 y




Finding The Derivative Of Log X Video Lesson Transcript Study Com
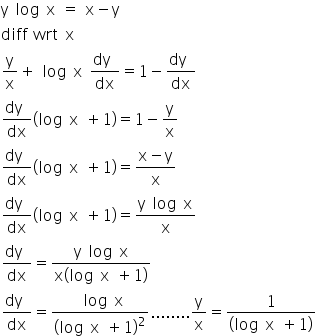



If Y Log X X Y Prove That Dy Dx Log X 1 Log X 2 Mathematics Topperlearning Com 2dolmeyy
If ∫ a 0 x 2 − 1 1 − x d x = − 1 2, then the value of a is equal to 2 If x denotes the greatest integer less than or equal to x, then the value of ∫ 0 2 ( x − 2 x) d x is equal to 3 The differential equation representing the family of curves y 2 = 2 c ( x 3 c), where c is a positive parameter, is ofFind dy/dx y^2=1/(1x^2) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set asIf 2x 2 3xy y 2 x 2y 8 = 0, then dy/dx is equal to If 3 ≤ 3t 18 ≤ 18, then which one of the following is correct?




If Y Log 1 Sin 2x 1 Tanx Find Dy Dx Maths Continuity And Differentiability Meritnation Com



What Is The Differentiation Of Log X 2 1 X 2 1 W R T X Quora
Question (1 point) Find dy when dr log(2) y = 1 log(x) = = (1 point) Use logarithmic differentiation to find the derivative y = x2 1 x2 2 y' = This question hasn't been solved yet Ask an expert Ask an expert Ask an expert done loading Show transcribed image text Expert AnswerTill infinite Find dy/dx Please give the solutionWrite in the form y=x^y since x^x^x^x is till infinite, we can consider it to be y, then take l Book a Trial With Our Experts × Given, We have to find the derivative of y Differentiating y with respect to x, Derivative of log x is 1/x Using Chain Rule of Differentiation, rosariomividaa3 and 13 more users found this answer helpful heart outlined Thanks 9 star




Find Dy Dx Given That Y Ln Squareroot X 2 1 Ln X Chegg Com




If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X 2 F I N D Dy Dx
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledLog y = log (x1)log (x2) 1/2log x 1/ydy/dx = 1/ (x1) 1/ (x2) 1/2x dy/dx= y 2x (x2)2x (x1) (x1) (x2)/2x (x1) (x2) dy/dx = { (x1) (x2)/√x} 2x^2–4x2x^2–2xx^23x2/2x (x1) (x2) dy/dx = (3x^2–3x2)/2x√x Answer 3K views · Find an answer to your question if ylogx = xy , prove thatdy/dx = logx/(1 logx)^2




If Y Log X 1 X2 1 2 Prove That Dy Dx 1 Log X 1 X2 1 2 1 1 X2 1 2 Mathematics Topperlearning Com Qsw6n0xx




If Y Log 5x Square 3x 2 Then Find Dy By Dx Brainly In
If 3 By 2 Plus I Root3 By 2 Power 50 Equal 3 25 X Iy Where X And Y Are Real Then The Ordered Pair X Y Is If 3 sin (xy) 4 cos (xy) = 5, then dy/dx = If 3 Tan Theta Tan Phi Is 1Suppose a dependent variable y represents a function f of an independent variable x, that is, = () Then the derivative of the function f, in Leibniz's notation for differentiation, can be written as (())The Leibniz expression, also, at times, written dy/dx, is one of several notations used for derivatives and derived functionsA common alternative is Lagrange's notationLet's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 log




If Y X 2 1 Log X 2 1 X Show That X 2 1 Dydx Xy 1 0



Solve 1 X 2d 2y Dx 2 1 X Dy Dx Y 2sin Log 1 X Sarthaks Econnect Largest Online Education Community
Manbar Singh, Meritnation Expert added an answer, on Manbar Singh answered this We have, y = log x cos x x 2 1 x 2 1 Let y = u v where u = log x cos x and v = x 2 1 x 2 1 Now, y = u v ⇒ dy dx = du dx dv dx 1 Let u = log x cos x ⇒ log u = cos x log log x ⇒ 1 u du dx = cos x × 1 x log x log log x sin Find an equation of the tangent line to the curve (x^2)(e^y)(ye^x)=4 at the point (2,0) asked in CALCULUS by payton Apprentice implicitdifferntiation If y=√ (x^21)log (1/x√ (11/x^2), find dy/dx Sarthaks eConnect Largest Online Education Community




If Y Log X Sqrt X 2 1 Prove That X 2 1 D 2 Y Dx 2 X Dy Dx 0 Youtube




Ex 6 2 7 Show That Y Log 1 X 2x 2 X Is An Increasing Fn
Find dy/dx y = natural log of x^2 y = ln (x2) y = ln ( x 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2)) d d x ( y) = d d x ( ln ( x 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Differentiate using the chain rule, which states that Share 1 VarunRawat answered this We have , y = log x cos x x 2 1 x 2 1 Let y = u v ⇒ dy dx = du dx dv dx 1 Now , u = log x cos x ⇒ log u = cos xSolution for Find dx y = 4 In x9 log 4x dy (Type an exact answer) dx Q A ferris wheel is 35 meters in diameter and boarded from a platform that is 1 meters above the groun A As per our company guidelines, we are supposed to answer only the first 3 subpartsKindly repost o



What Will Be The Value Of D Dx Log 1 X 2 Quora




If Y Log X Sqrt 1 X 2 Prove That Sqrt 1 X 2 Dy Dx 1 Youtube
If dy/dx=2y^2 and if y= 1 when x=1, then when x=2 y=? Ex 53, 11 Find 𝑑𝑦/𝑑𝑥 in, 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) , 0 < x < 1 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) Putting x = tan θ ySolutionShow Solution It is given that `y=log xsqrt (x^2a^2)` Differentiating equation (1) with respect to x, we get `dy/dx= (1x/sqrt (x^2a^2))/ (xsqrt (x^2a^2))` `dy/dx=1/sqrt (x^2a^2) (2)` `xdy/dx=x/sqrt (x^2a^2) (3)` Again differentiating equation (2) with respect to x, we get




Ex 5 5 7 Differentiate The Function Log X X X Log X



Solve X Dy Dx Y Log Y Log X 1 Studyrankersonline
If y = 2^x, find dy/dx Q If y = 2^x, find dy/dx ANSWER 1) Take Logs of both sides of our equation y = 2^x So we get log (y)=log (2^x) 2) Apply relevant log rule to rhs Log rule log (a^b) = b log (a) nb the dot between b and log (a) represents x / multiply / times ) So we get log (y) = x log (2)




If Y Logsqrt 1 Sin 2 X 1 Sinx Find Dy Dx



5 Derivative Of The Logarithmic Function




Q37 If Y Log X X 2 A 2 Then Show That X 2 A 2 D 2 Y Dx 2 X Dy Dx 0 Youtube




Y X2 1 1 2 Log 1 X 1 1 X2 1 2 Find Dy Dx Maths Continuity And Differentiability Meritnation Com
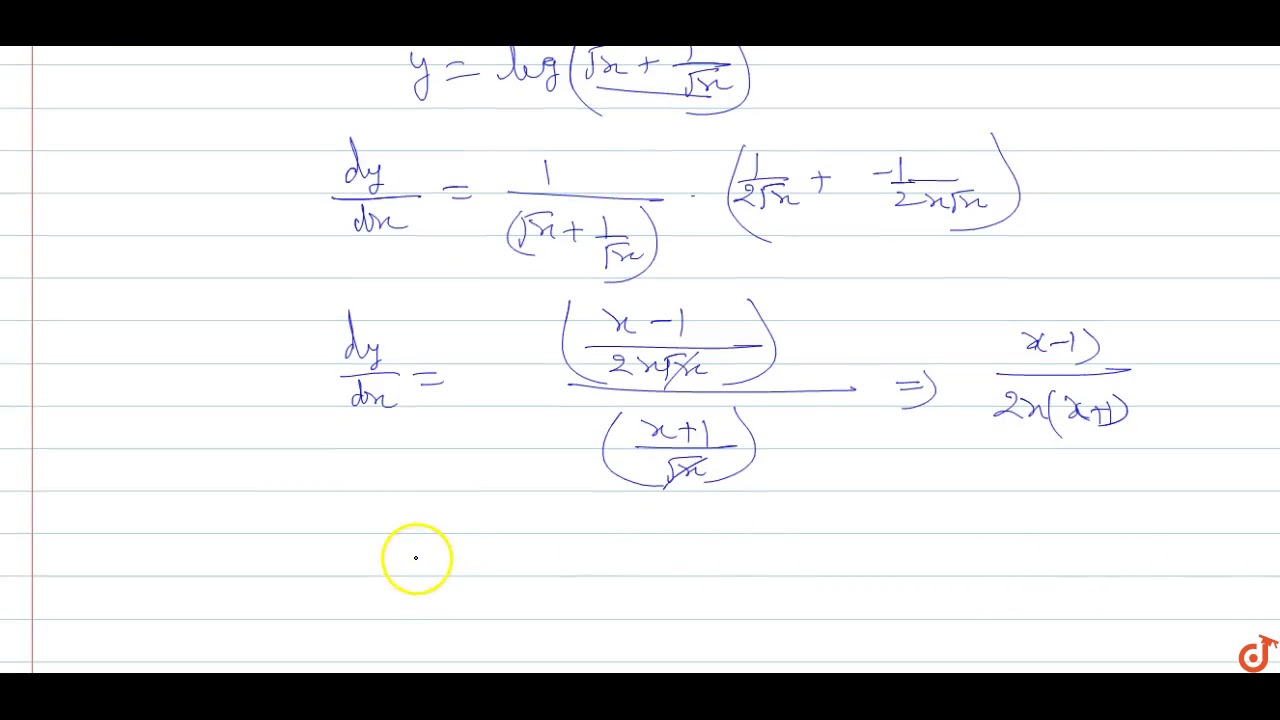



If Y Log Sqrt X 1 Sqrt X Prove That Dy Dx X 1 2x X 1 Youtube



What Is The Differentiation Of Log X 2 1 X 2 1 W R T X Quora



1




Y Log X Root 1 X2 Prove That 1 X2 D2y Dx2 X Dy Dx 0 Brainly In



Differentiate Log X X2 A W R T X Studyrankersonline



If Y Log 1 Cos X 1 Cos X How Can You Prove That Dy Dx 2cosec X Quora




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1
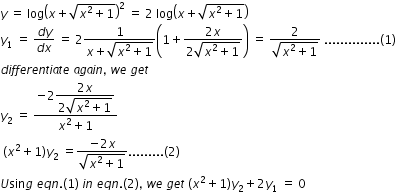



If Y Log X Rt X2 1 2 Show That 1 X2 Y2 Xy1 2 Mathematics Topperlearning Com Uz7rkazz




If Y X 2 1 Log 1 X 1 1x 2 Then Find Dy Dx Brainly In
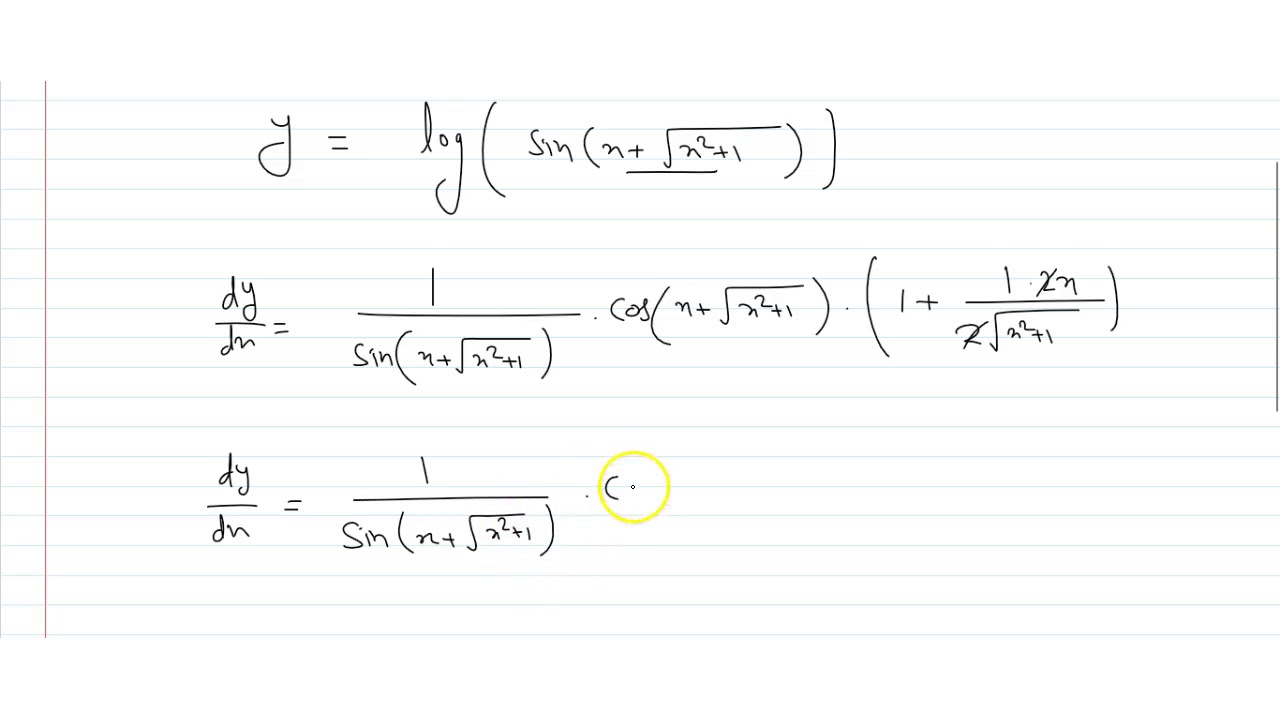



If Y Log Sin X Sqrt X 2 1 Find Dy Dx Youtube
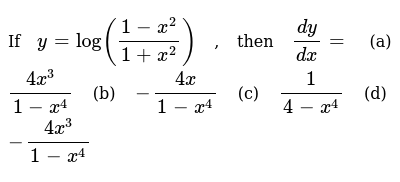



If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 4x 1 X 4 C 1 4 X 4 D 4x 3 1 X 4




If Y Log X X 2 A 2 X 2 A 2 X Find Dy Dx Brainly In




Section 3 1 6 9 16 25 Section 3 2 7 11 15 Chegg Com




If Y Log 1 2t 2 T 4 X Tan 1 T Find Y Teachoo



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora



How To Find Cf And Pi D 2 Y Dx 2 1 X Dy Dx 12 Logx X 2 Quora




If Y Root X 2 1 Log 1 X Root 1 1 X 2 Find Dy Dx Maths Continuity And Differentiability Meritnation Com



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community




Ex 5 5 2 Differentiate Root X 1 X 2 X 3 X 4 X 5
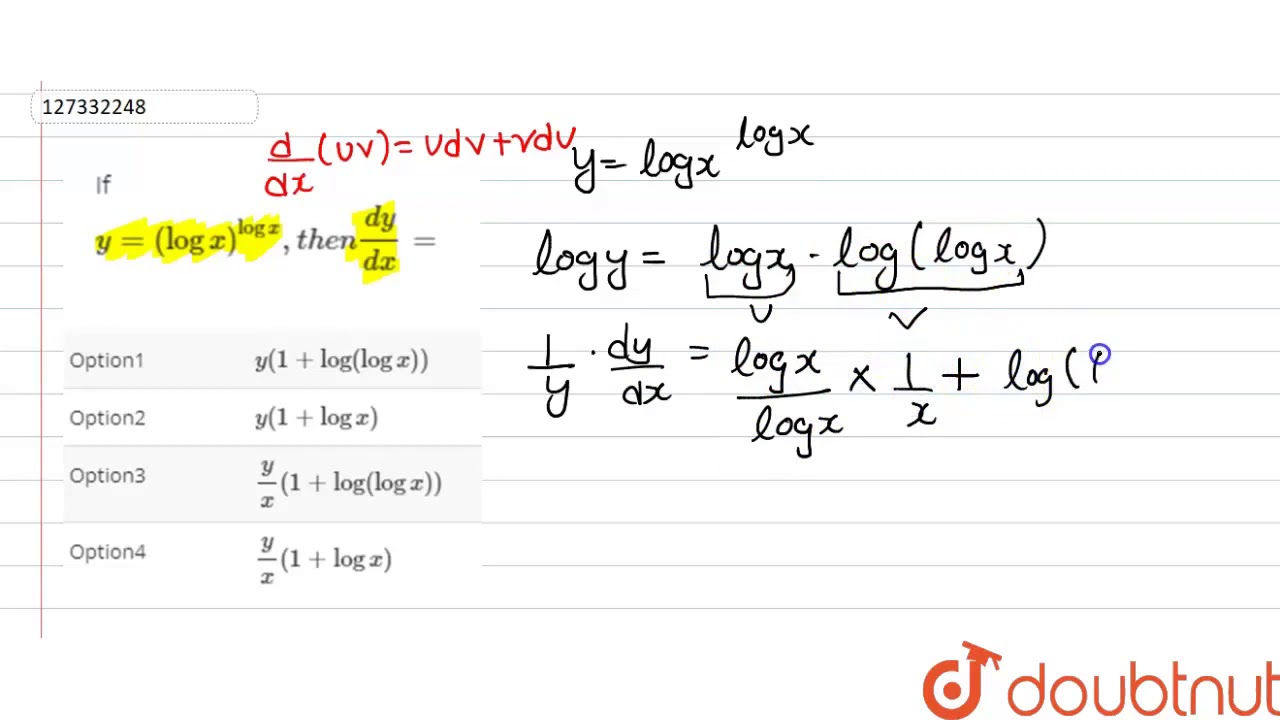



If Y Log X Logx Then Dy Dx Youtube




If Y Log 1 X 2 1 X 2 Then Dy Dx Is Equal To




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If Y Log 1 1 X Then 1 Dy Dx



What Is The Derivative Of X 2 Log X Quora



Q Tbn And9gctlpwtqpeqpxc M 4azweuyu3w0v85my8luxgzbm9ccv Ohozkr Usqp Cau




Y Log 1 Sin X 1 Sin X Then Dy Dx



If X Y E X Y Show That Dy Dx Logx Log Xe 2 Sarthaks Econnect Largest Online Education Community




Y Log 3x 2 2x 1 F I N D Dy Dx




If Y Log X Root X2 1 Then Prove That X2 1 Dy Dx X Dy Maths Meritnation Com



If Yx Ey X Prove That Dy Dx 1 Log Y 2 Log Y Studyrankersonline




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If Y Log 1 X 21 X 2 Then Dydx Is Equal To




Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which




Derivatives Of Logarithmic Functions Find Dy Dx Y Chegg Com




If Y Log X Root X2 1 Then Prove That X2 1 Dy Dx X Dy Dx 0 Brainly In




If E Tanx Logx Tanx Then Find Dy Dx



If Xy E X Y Then Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community



1




If Y Log Tan X 2 Find Dy Dx




If Y Log 1 Cos2 X 1 E2x 1 2 Show That Dy Dx E2x 1 E2x Sin X Cos X 1 Cos2 X Show Each And Every Step Mathematics Topperlearning Com Idjkxezz




If Y Log Sqrt X 2 X 1 X 2 X 1 1 2sqrt3 Tan 1 2x 1 Sqrt3 Tan 1 2x 1 Sqrt3 Then Prove That Dy Dx 1 X 4 X 2 1




Engineering Mathematics Notes




If Y Log 1 X 1 X 1 4 1 2tan 1 X T H E N Dy Dx Youtube




5 Derivative Of The Logarithmic Function




If Y Log Log Logx 3 Then Dy Dx
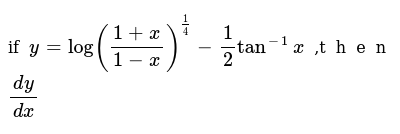



If Y Log 1 X 1 X 1 4 1 2tan 1 X T H E N Dy Dx




Solve The Initial Value Problem Dy Dx Y 1 X 3 Chegg Com



Solve 1 X 2d 2y X 2 1 X Dy Dx Y 4cos Log 1 X Sarthaks Econnect Largest Online Education Community




Hi My Question Is If Y Log X 1 X 2 1 2 2 Find Dy Dx And D 2y Dx 2 Maths Continuity And Differentiability Meritnation Com



Zvvp4trj5evbm



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community
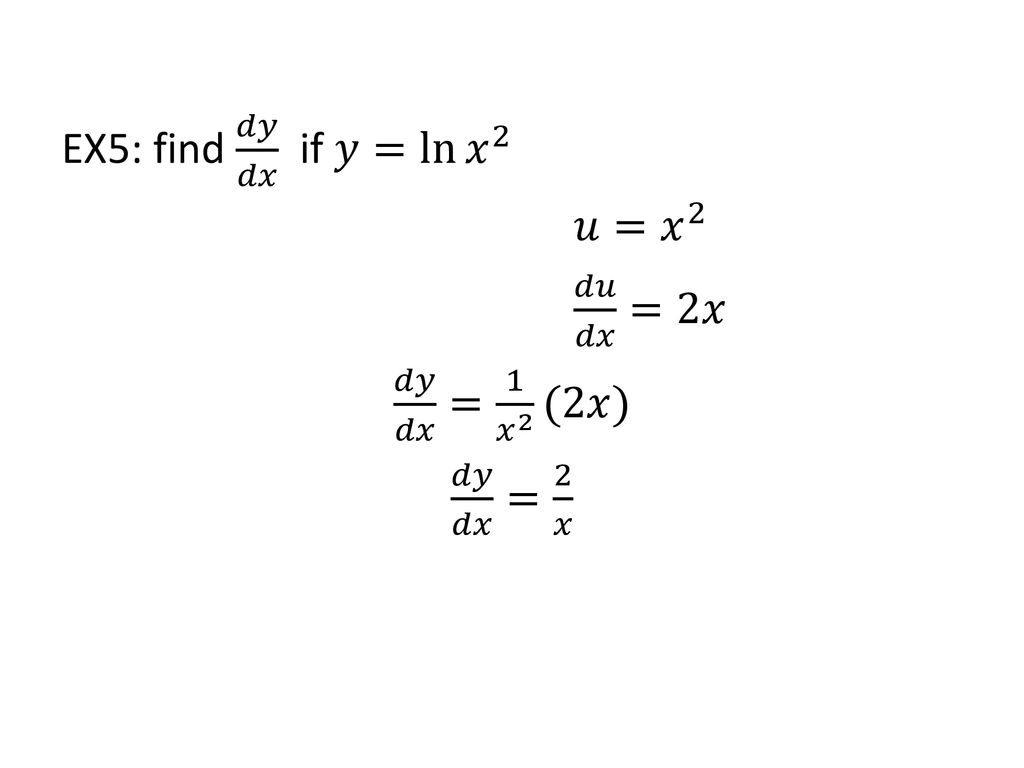



Derivatives Of Ppt Download




If X 1 T And Y Log T Find Dy Dx Brainly In




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 4x 1 X 4 C 1 4 X 4 D 4x 3 1 X 4
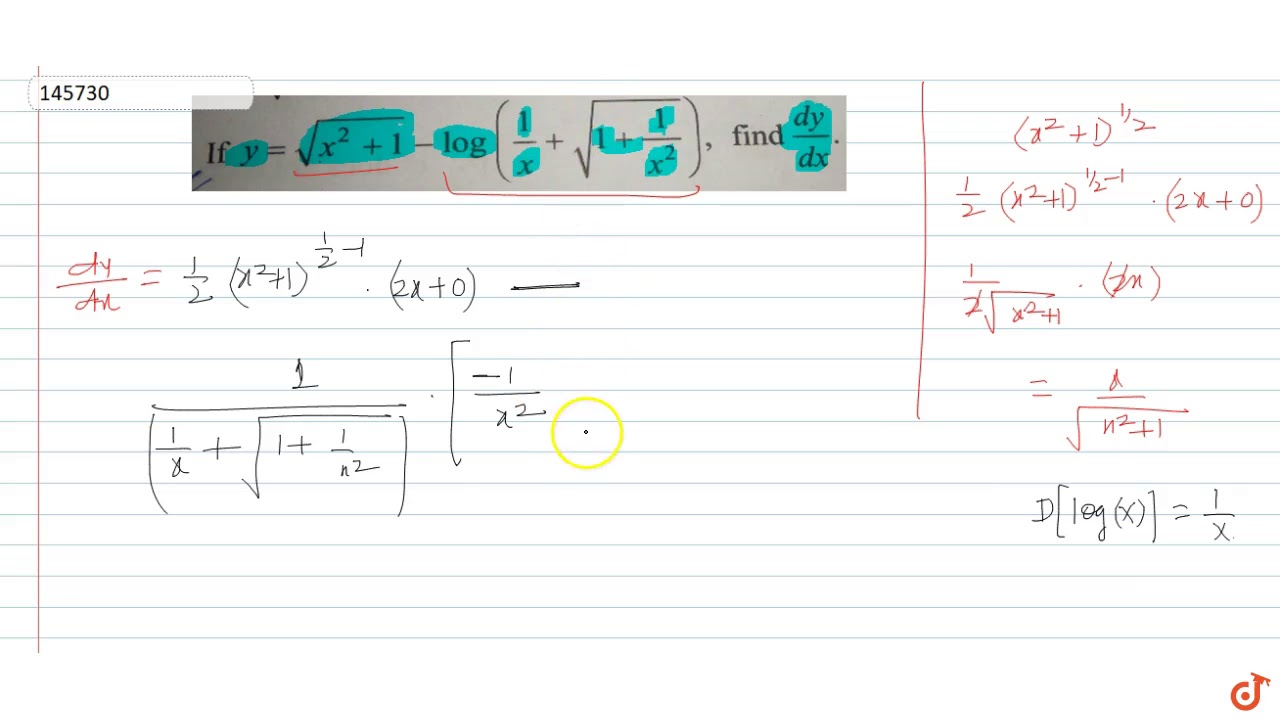



Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx Youtube




Y Log 1 X 1 X Find Dy Dx Brainly In



If Y Log Cos X Sin X Log Sin X Cos X 1 Sin 1 2x 1 X 2 Find Dy Dx At X P 4 Sarthaks Econnect Largest Online Education Community




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which



Qkpba2ytmixmim




If Y Log X Sqrt X 2 A 2 Show That X 2 A 2 D 2 Y Dx 2 X Dy Dx 0 Youtube




What Is The Derivative Of 1 Logx Quora
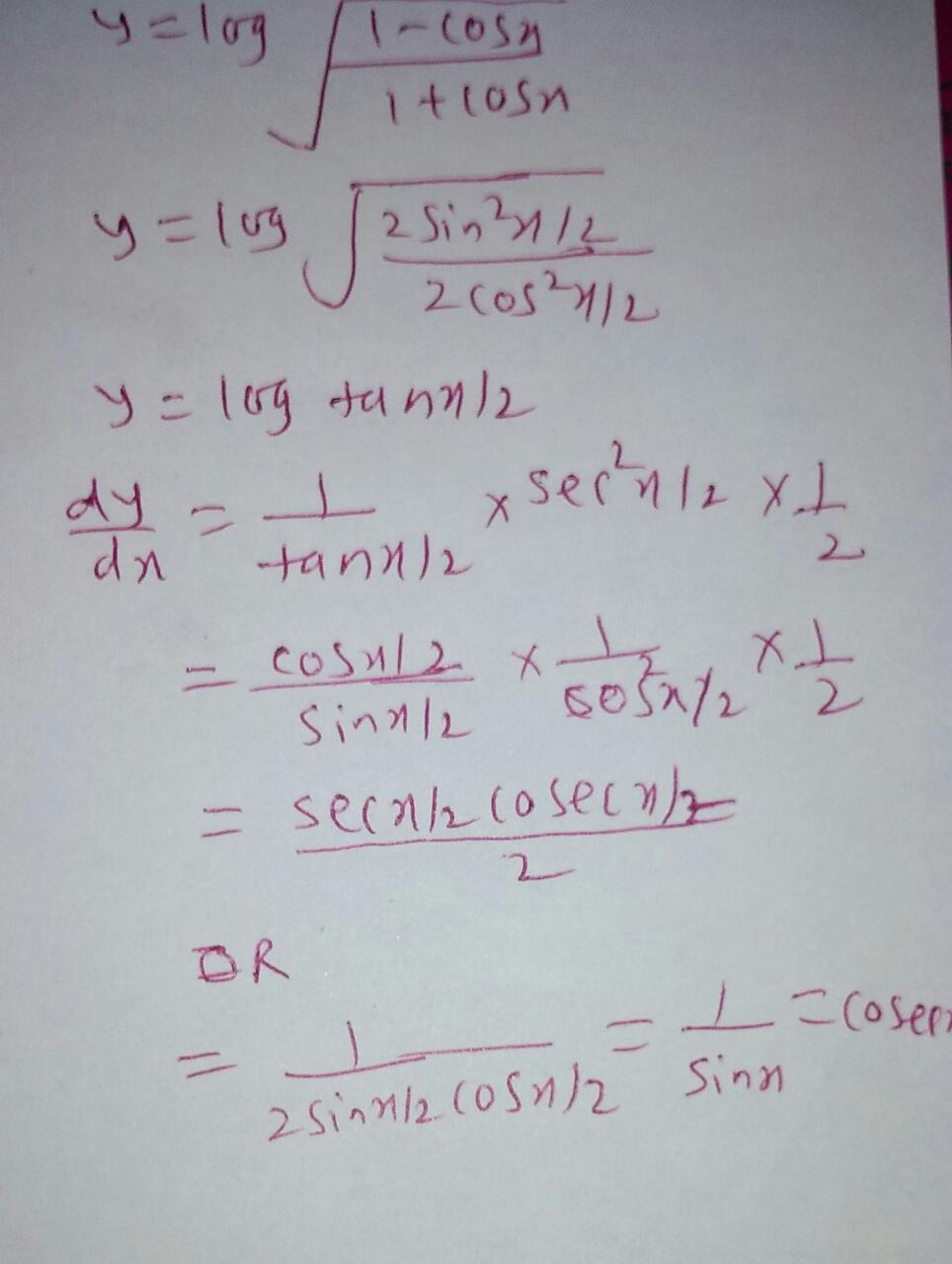



If Y Log 1 Cos X 1 Cos X 1 2 Show That Dy Dx Cosec X Mention Each And Every Formula And Minute Details Mathematics Topperlearning Com H7b68mm




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1
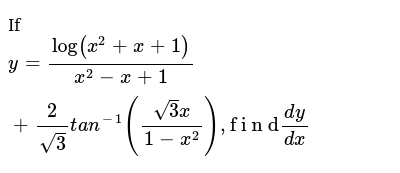



If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X 2 F I N D Dy Dx




If Y Log X Sqrt X 2 A 2 Show That X 2 A 2 D 2y Dx 2 X Dy Dx 0 Youtube




Y Log X X 2 25 X 2 25 X Find Dy Dx




Ex 6 2 7 Show That Y Log 1 X 2x 2 X Is An Increasing Fn




Differentiate The Function With Respect To X X Xcosx X 2 1 X 2 1 Mathematics Shaalaa Com




If Y Log Sin X 2 1 Prove That Dy Dx Xcot X 2 X 1 Brainly In




If Y Log E X X 2 X 2 3 4 Show That Dy Dx X 2 1 X 2 1 Maths Determinants Meritnation Com



If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 1 4 X 4 C 1 4 X 4 D 4x 3 1 X 4 Sarthaks Econnect Largest Online Education Community



What Will Be The Value Of D Dx Log 1 X 2 Quora



1




Engineering Mathematics Notes




Find The Derivatives W R T X Y 1 X 1 2x 1 3x 2 Youtube




Can Anyone Please Help Me Do This If Log X Aˆs 1 X2 2 Show That 1 X2 D2y Dx2 X Dy Dx 2 0 Maths Differential Equations Meritnation Com



0 件のコメント:
コメントを投稿